Parte 1. La teoría cuántica y la consciencia

2.1. El método científico

El método científico tiene cuatro componentes principales:

1. La suposición de una realidad externa y objetiva que puede observarse.
2. Experimentos cuantitativos sobre la realidad externa y objetiva para determinar sus propiedades perceptibles, y el uso de la inducción para descubrir sus principios generales. Esto fue primero sistemáticamente expresado por el estadista inglés Francis Bacon (1561-1626) en su Novum Organum, publicado en 1620.
3. Analizar experimentos cuantitativos con precisión matemática. Se cree que el científico italiano Galileo Galilei (1564-1642) fue el primero en establecer claramente que las leyes de la naturaleza son matemáticas. Se le ha denominado de forma muy diversa como el "padre de la astronomía observacional moderna", el "padre de la física moderna" y el "padre de la ciencia moderna". En su libro de 1632, Diálogo sobre los Dos Principales Sistemas del Mundo, defendió el modelo copernicano del sistema solar contra el sistema tradicional de Ptolomeo. Fue declarado culpable de herejía por esto por la Iglesia Católica en 1633.
4. La validación de los resultados de estas mediciones mediante una comunicación y publicación generalizada para que otros científicos puedan verificarlos independientemente. Aunque los científicos a lo largo de la historia han comunicado y publicado sus resultados, el primer científico en expresar la necesidad de publicar los detalles de sus métodos experimentales para que otros científicos pudieran repetir sus mediciones fue el químico inglés Robert Boyle (1627-1691), quién fue grandemente influenciado por las opiniones de Bacon.
5. Intuir y expresar las leyes matemáticas que describen la realidad externa y objetiva. Las leyes más universales son aquéllas de la física, la ciencia más fundamental. El filósofo inglés Isaac Newton (1642-1727) fue el primer científico en expresar leyes que fueron consideradas de aplicación universal en todos los sistemas físicos.

Los cuatro últimos de estos componentes (¡tres de ellos por ingleses!) fueron todos desarrollados en un período notablemente breve desde 1620 a 1687.

2.2. Las leyes de newton y el determinismo

Para entender la física cuántica, debemos entender primero la física clásica para que podamos apreciar las diferencias entre ambas.

Hay dos suposiciones fundamentales en la física clásica. La primera suposición fundamental es que el mundo objetivo existe independientemente de cualquier observación que se haga de él. Usando una analogía popular, un árbol que cae en el bosque produce un sonido ya sea que esté o no presente alguien para oírlo. Aunque es posible que las observaciones del mundo objetivo puedan afectarlo, su independencia garantiza que no necesariamente lo afectan.

Preguntas: ¿Cómo serían de diferentes nuestras vidas si no hubiera una realidad objetiva externa y nosotros no lo supiéramos? ¿Y si lo supiéramos?

La segunda suposición fundamental de la física clásica es que la posición y la velocidad de un objeto pueden medirse sin límites en su precisión excepto para los de los instrumentos de medición. En otras palabras, el mundo objetivo es un mundo preciso sin incertidumbre intrínseca en él. Como veremos más tarde, la teoría cuántica renuncia a estas dos suposiciones fundamentales.

Isaac Newton fue el primer científico importante en llevar a cabo experimentos fundamentales y elaborar comprensivas teorías matemáticas para explicarlos. Inventó una teoría de la gravedad para explicar las leyes del astrónomo y matemático alemán Johannes Kepler (1571-1630) que describe las órbitas planetarias, aprovechó los famosos experimentos de caída libre desde la torre inclinada de Pisa del científico italiano Galileo Galilei (1564-1642), e inventó el cálculo para dar un esquema matemático apropiado a las leyes de movimiento que él descubrió. Newton se consideraba a sí mismo como un filósofo naturalista, pero la costumbre contemporánea le otorgaría el título de físico. De hecho, él, probablemente más que cualquier otro científico, estableció la física como una disciplina científica separada debido a sus esfuerzos por expresar sus conclusiones desde el punto de vista de las leyes físicas universales. Algunos piensan que él fue el científico más grande que ha vivido jamás. En 1687 a la edad de 44 años publicó su Philosophiae Naturalis Principia Mathematica (Principios Matemáticos de la Filosofía Natural) en donde él expuso sus leyes del movimiento y la gravitación.

Sus tres leyes del movimiento pueden describirse como sigue:

1. Primera Ley o Ley de Inercia: Todo cuerpo permanece en su estado de reposo o de movimiento rectilíneo uniforme a menos que otros cuerpos actúen sobre él.
2. Segunda Ley o Principio Fundamental de la Dinámica: La fuerza que actúa sobre un cuerpo es directamente proporcional a su aceleración.
3. Tercera Ley o Principio de acción-reacción: Cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero una fuerza igual y de sentido opuesto.

Para utilizar estas leyes, deben conocerse las propiedades de las fuerzas que actúan en un cuerpo. Como ejemplo de una fuerza y sus propiedades, la ley de Newton de la gravitación establece que la fuerza gravitatoria entre dos cuerpos, como la tierra y la luna, es proporcional a la masa de cada cuerpo y es inversamente proporcional al cuadrado de la distancia entre ellos. Esta descripción de la fuerza gravitatoria, cuando se usa junto con la segunda ley de Newton, explica por qué las órbitas planetarias son elípticas. Debido a la tercera ley de Newton, la fuerza que actúa en la tierra es igual y opuesta a la fuerza que actúa en la luna. Ambos cuerpos constantemente están cambiando sus velocidades y direcciones debido a la fuerza gravitatoria que actúa continuamente en ellos.

Otro ejemplo es la fuerza gravitatoria que actúa entre la tierra y mi cuerpo. Siempre que mi cuerpo esté estacionario, debe haber otra fuerza que actúa en él, sino la primera ley de Newton no sería correcta. Si yo estoy sentado en una silla, esa otra fuerza es una fuerza ascendente que actúa en mi cuerpo por la silla, y esto mismo anula la fuerza gravitatoria que actúa en mi cuerpo por la tierra. La fuerza que actúa en mi cuerpo por la gravedad (mi peso) es igual y opuesta a la fuerza que actúa en mi cuerpo por la silla, y viceversa.

Preguntas: ¿Cuál es nuestra sensación inmediata de la fuerza gravitatoria? ¿Cuál sería si estuviéramos en caída libre? ¿Cuáles son las fuerzas en un automóvil si está acelerando hacia adelante? ¿Cuáles son si se está moviendo con velocidad constante en círculo?

Durante más de 200 años, después de muchos experimentos que abarcan todos los temas accesibles de naturaleza macroscópica, las leyes de Newton llegaron a considerarse por los físicos y gran parte de la sociedad como las leyes que eran obedecidas por todos los fenómenos del mundo físico. Tuvieron éxito explicando todos los movimientos, desde los planetas y estrellas hasta las moléculas de un gas. Este éxito universal condujo a la creencia generalizada en el principio del determinismo, que dice que, si el estado de un sistema de objetos (incluso todos los que abarca el universo) es conocido con precisión en un momento dado, como ahora, el estado del sistema en cualquier momento del futuro puede en principio predecirse con precisión. Para los sistemas complejos, la matemática exacta podría ser demasiado complicada, pero eso no afectó al principio. Finalmente, se pensó que este principio podría aplicarse a los seres vivos así como a los objetos inanimados. Se pensaba que este mundo determinista era completamente mecánico, sin espacio para el libre albedrío, de hecho sin espacio incluso para cualquier pequeña desviación de su último destino. Si había un Dios en este mundo, su papel estaba completamente limitado a poner en movimiento todo el asunto en el principio.

Intrínseca al principio del determinismo estaba la suposición de que el estado de un sistema de objetos podría describirse con precisión en todo momento. Esto significaba, por ejemplo, que la posición y velocidad de cada objeto podía especificarse exactamente, sin ninguna incertidumbre. Sin tal exactitud, la predicción de futuras posiciones y velocidades sería imposible. Después de muchos, muchos experimentos parecía claro que sólo la inevitable imprecisión en los instrumentos de medición limitaba la exactitud de una medición de velocidad o posición, y nadie dudaba que las precisiones pudieran mejorar sin límite cuando las técnicas de medición mejoraran.

Preguntas: ¿Cómo serían nuestras vidas de diferentes si el mundo fuera determinista pero no lo supiéramos? ¿Y si lo supiéramos?
Suponga que acepta el principio del determinismo como verdad. ¿Cómo se sentiría entonces acerca de sus sentimientos, decisiones y acciones? ¿Y acerca de los sentimientos, decisiones y acciones de otras personas? ¿Cómo afectaría a sus juicios sobre usted y los demás?

2.3. Termodinámica y mecánica estadística; la entropía y la dirección del tiempo

La termodinámica es una rama de la física que estudia los efectos de los cambios de temperatura, presión y volumen de los sistemas físicos a un nivel macroscópico. La mecánica estadística es la teoría que describe las propiedades macroscópicas como presión, volumen y temperatura de un sistema en función del promedio de las propiedades de sus componentes microscópicos, los átomos y moléculas. La termodinámica y la mecánica estadística tratan ambas de predecir las mismas propiedades y describir los mismos procesos, la termodinámica desde un punto de vista macroscópico, y la mecánica estadística desde un punto de vista microscópico.

En 1850, el físico alemán Rudolf Clausius (1822-1888) propuso la primera ley de la termodinámica, que establece que la energía puede convertirse de una forma en otra, como la energía en forma de calor en la rotación mecánica de una turbina, pero siempre se conserva. Desde 1905 cuando el físico alemán-suizo-americano Albert Einstein (1879-1955) inventó la teoría especial de la relatividad, sabemos que la energía y la materia pueden convertirse una en otra. Por eso, la primera ley realmente se aplica conjuntamente a ambas, la materia y energía. Esta ley es probablemente la ley más fundamental en la naturaleza. Se aplica a todos los sistemas, no importa si es pequeño o grande, simple o complejo, viviente o inanimado. Nosotros no pensamos que no se infrinja nunca en cualquier parte en el universo. Nunca se propone una nueva teoría física sin verificar y ver si confirma esta ley.

Pregunta: ¿Cuáles son algunos ejemplos cotidianos de la primera ley de la termodinámica?

La segunda ley de la termodinámica puede plantearse de varias maneras. La primera declaración de ella, hecha por Rudolf Clausius en 1850, es que el calor puede fluir espontáneamente desde un objeto caliente a uno frío, pero no puede pasar espontáneamente de uno frío a uno caliente. La segunda declaración de la segunda ley fue hecha más tarde por el físico escocés William Thomson Kelvin (1824-1907) y el físico alemán Max Planck (1858-1947): La energía en forma de calor no puede ser completamente transformada en energía mecánica, pero la energía mecánica puede ser completamente transformada en energía de calor.

Pregunta: ¿Cuáles son algunos ejemplos cotidianos de la segunda ley de la termodinámica?

La tercera declaración de la segunda ley depende de un nuevo concepto, el de la entropía. Para hablar de la entropía, primero hablaremos del número de ordenamientos distinguibles de un sistema, del cual se deriva el concepto de entropía. Algunos lectores pueden desear saltarse esta exposición e ir directamente a la definición de entropía que se da después.

• Ejemplo #1: Imagina una caja dividida en dos compartimientos, cada uno de los cuales puede sostener sólo una pelota. Ponga una pelota en uno de los compartimientos. Claramente, el número de formas que puedes hacer esto es dos —la pelota puede colocarse en cualquiera de los compartimientos. (Matemáticamente, éste es el número de combinaciones de dos objetos tomados de uno en uno; esto es dado por el coeficiente binomio).
• Ejemplo #2: Si hay tres compartimientos, el número de formas que puedes poner una pelota es tres (el número de combinaciones de tres objetos tomados de uno en uno).
• Ejemplo #3: Si hay cuatro compartimientos, el número de formas que puedes poner una pelota es cuatro (el número de combinaciones de cuatro objetos tomados de uno en uno).
• Ejemplo #4: Ahora ponemos dos pelotas idénticas en una caja con dos compartimientos. El número de formas que puedes hacer esto es sólo una (el número de combinaciones de dos objetos tomados de dos en dos) porque si las pelotas se intercambian, no hay ninguna diferencia discernible en los ordenamientos.
• Ejemplo #5: Ahora ponemos dos pelotas idénticas en una caja con tres compartimientos. El número de formas que puedes hacerlo puede considerarse de la siguiente manera:
  1. La primera pelota en el compartimiento #1, la segunda en uno de los otro dos. Esto suma dos.
  2. La primera pelota en el compartimiento #2, la segunda en el #1 o en el #3. Pero el primer arreglo es idéntico al primer arreglo en a), así que no cuenta. El segundo arreglo es nuevo, así que lo contamos. Si ahora la primera pelota se pone en #3, la segunda puede ponerse en #1 o #2, pero éstos no son nuevos, así que no los contamos.
• Por lo tanto, el número total de ordenamientos distinguibles para dos pelotas idénticas en tres compartimientos es tres (el número de combinaciones de tres objetos tomados de dos en dos).
• Ejemplo #6: Ahora ponemos dos pelotas idénticas en una caja con cuatro compartimientos. Contamos el número de formas posibles como sigue:
  1. La primera pelota en #1, la segunda en #2, #3, o #4. Esto suma tres.
  2. La primera pelota en #2, la segunda en #1, #3, o #4. El primero es igual que el primer arreglo en a), así que hay dos nuevos ordenamientos distinguibles.
  3. La primera pelota en #3, la segunda en #1, #2, o #4. Sólo el último arreglo es nuevo, así que hay un arreglo distinguible adicional.
  4. La primera pelota en #4, la segunda en #1, #2, o #3. Cada uno de estos ordenamientos es idéntico a a), b), o c), así que éstos no son nuevos.
• Así, el número total de ordenamientos distinguibles para dos pelotas idénticas en cuatro compartimientos es seis (el número de combinaciones de cuatro objetos tomados de dos en dos).
• Ejemplo #7: Ahora ponemos dos pelotas sólo en los tres primeros de cuatro compartimientos. Esto es idéntico al Ejemplo #5 sólo que ahora hay dos pelotas en cuatro compartimientos en lugar de dos pelotas en tres compartimientos. El número de ordenamientos distinguibles es ahora de tres con tal que sepamos que las pelotas están en los primeros tres compartimientos. Este ejemplo muestra que el número de ordenamientos distinguibles no sólo depende del número de pelotas y compartimientos, sino también de cómo las pelotas se distribuyen en los compartimientos.
• Los métodos de probabilidades nos permiten calcular el número de ordenamientos distinguibles en cualquier número de compartimientos ya sea que las pelotas sean idénticas o no, y para cualquier distribución de las pelotas. Para un número dado de compartimientos y de pelotas idénticas, el número de ordenamientos distinguibles es más pequeño (igual a uno) cuando el número de pelotas es igual que el número de compartimientos (ejemplo #4). Esto correspondería a un puro material sólido cristalino. Para un número dado de compartimientos y de pelotas idénticas, el número de ordenamientos distinguibles es máximo cuando el número de pelotas es igual a la mitad del número de compartimientos (ejemplo #6). Esto correspondería a un gas muy comprimido. Para un gas rarificado, el número de compartimientos (cada uno igual al tamaño de una molécula) es inmensamente más grande que el número de moléculas, y el número de ordenamientos distinguibles es mucho mayor que uno (ejemplo #3) pero menos del máximo (ejemplo #6).

Ahora podemos definir la entropía. La entropía se relaciona con (en realidad, es proporcional al logaritmo de) el número total de posibles ordenamientos distinguibles del sistema (en un espacio seis-dimensional de la posición-velocidad – tres dimensiones para la posición y tres para la velocidad – en lugar de en el espacio tridimensional de la posición del ejemplo anterior). La entropía aumenta rápidamente cuando aumentamos el volumen del sistema, el número de objetos en él, y la energía total de los objetos. Para un sistema macroscópico, digamos 10²³ partículas, la entropía es enormemente más grande que para el sistema de dos pelotas descrito anteriormente. La entropía también es más grande cuando los objetos son uniformemente distribuidos (ejemplo #6) que cuando se agrupan juntos (ejemplo #7). Resulta que también es más grande cuando la energía así como la masa es uniformemente distribuída. Puesto que la energía se relaciona con la temperatura, la entropía es mayor cuando la temperatura es uniforme, y aumenta cuando aumenta la temperatura.

La entropía se relaciona con la cantidad de desorden y orden en el sistema. La entropía decreciente es equivalente al desorden o desorganización decreciente (orden u organización creciente) de un objeto o sistema (ejemplo #7); mientras que la entropía creciente es equivalente al desorden o desorganización creciente (orden u organización decreciente) (ejemplo #6).

Resulta que la segunda ley de la termodinámica puede establecerse de la siguiente manera: Los procesos naturales de un sistema macroscópico aislado normalmente prosiguen en la dirección de máxima probabilidad (el desorden máximo) que es la dirección del número máximo de ordenamientos distinguibles del sistema. (Es muy improbable, aunque no totalmente imposible, que prosigan en la dirección opuesta).  La dirección progresiva del tiempo es la dirección en que la entropía se incrementa. Por lo tanto, la segunda ley de la termodinámica puede replantearse desde el punto de vista de la entropía: Los procesos naturales de un sistema macroscópico aislado siempre prosiguen en la dirección de la entropía creciente (el desorden). En la física clásica, esto define la dirección progresiva del tiempo. En la Sección 6.4, veremos lo que determina esta dirección en la física cuántica. (Hay que advertir que hemos enfatizado que la segunda ley sólo se aplica a un sistema que está aislado del resto del universo, o del universo entero).

La segunda ley se basa en nuestras observaciones de la dirección en el tiempo de los procesos naturales. Decimos que esta dirección depende del universo que prosigue en el tiempo de un estado de baja entropía a un estado de mayor entropía, pero en la física clásica, la creciente dirección de la entropía es idéntica a la dirección de avance del tiempo. No podemos distinguir una de la otra. Es una tautología decir que la entropía aumenta con el tiempo porque el aumento de la entropía no puede distinguirse de la dirección de avance del tiempo. Sin embargo, en la física cuántica, la dirección del tiempo está determinada por la naturaleza de un evento cuántico (véase el Capítulo 6).

Nota: El hecho de que la dirección de avance del tiempo es la dirección del aumento de entropía implica que el universo empezó en un estado mucho más bajo de entropía que el de hoy. Lo que causó que la entropía fuera tan baja cuando el universo comenzó no se conoce. Este es un tema de intensa investigación en la cosmología teórica.

La dirección del tiempo también puede inferirse de las primeras dos declaraciones de la segunda ley de la termodinámica: 1) El flujo unidireccional de calor de los cuerpos calientes a fríos, y 2) la posibilidad de conversión total de la energía mecánica a energía de calor, pero no al revés.

Un error que comenten algunas personas es pensar que la segunda ley se aplica a objetos individuales o sistemas, como los automóviles, plantas, o los cuerpos humanos, aunque no estén aislados del resto del universo, y que ésta es la razón de que tales objetos decaigan y se desintegren con el tiempo. Ésta es una falacia, no obstante, porque la segunda ley no impide que la entropía de un objeto individual disminuya continuamente con el tiempo y así volverse más ordenado y organizado mientras recibe energía de algo más en el universo cuya entropía continúa aumentando. En nuestro sistema solar, está principalmente la entropía del sol que continuamente aumenta mientras su combustible se quema y se vuelve más desordenado.

La discusión anterior se basa en nuestra comprensión del tiempo objetivo dentro de la física clásica. No dice nada acerca de nuestra sensación subjetiva del paso del tiempo. Independientemente de lo que diga el reloj, todos experimentamos el paso del tiempo más rápido en algunas circunstancias que en otras. Nuestra experiencia de duración depende de nuestra percepción del grado de cambio y de nuestro estado emocional que nos acompaña ("El tiempo pasa más rápido cuando uno se está divirtiendo", "¡Cómo pasa el tiempo!").

Pregunta: ¿Cree que la entropía de su cuerpo está disminuyendo mientras envejece, o está aumentando?

El economista Jing Chen ha escrito que la selección natural en la evolución biológica puede ser vista como una fuerza hacia los estados de baja entropía de la mente humana a costa de aumentar la entropía del universo (véase en The Entropy Theory of Human Mind en http://web.unbc.ca/~chenj/1.pdf):

• La gente suele creer que las leyes físicas sólo tienen una utilidad limitada en la comprensión del comportamiento humano, porque nuestra mente es libre. Sin embargo, la mente humana está determinada por la selección natural y la selección sexual. Los organismos vivos necesitan extraer la baja entropía del medio ambiente, para defender sus fuentes de baja entropía y para reducir la difusión de la baja entropía. La lucha por permanecer en los estados de baja entropía se llama selección natural. En las sociedades humanas, la agricultura es la principal fuente de baja entropía. Parte de los sistemas de atención sanitaria tienen por objeto la defensa de nuestras propias fuentes de baja entropía del acceso de virus y bacterias. Las fuerzas militares se han establecido para extraer la baja entropía de otros y para defender las fuentes propias de baja entropía. El vestido y la vivienda reduce la difusión de la baja entropía.
• La selección sexual es la lucha entre los individuos de un sexo, generalmente los machos, para comunicar su atractivo al otro sexo, a fin de asociarse para la reproducción. Los seres humanos, así como otras especies que se reproducen sexualmente, son los descendientes afortunados de las primeras especies que se reprodujeron sexualmente hace unos mil millones de años. Para que el sistema de comunicación tenga éxito en diferentes tipos de ambientes en tan largo tiempo, el modo de comunicación tiene que ser simple, estable y universal. Dado que la ley de la entropía, que establece que los sistemas cerrados tienden a estados de mayor entropía, es la ley más universal de la naturaleza, es natural que el despliegue de los bajos niveles de entropía evolucione como la señal universal de la atracción en el proceso de selección sexual.
• Dado que tanto la selección natural la selección sexual favorecen el estado de baja entropía, la búsqueda de baja entropía se convierte en el motivo principal de la mente humana y de la mente de los animales. De hecho, el estado de baja entropía es la principal forma de divulgación para la mayoría de las especies que se reproducen sexualmente. Gran tamaño corporal, colores y formas de plumas de alta complejidad con gran cantidad de contenido de información y de las estructuras exóticas son todas diferentes representaciones de los estados de baja entropía. Puesto que un evento de baja probabilidad corresponde a un estado de baja entropía, una novedad es a menudo atractiva en la competencia por la reproducción. En general, se reconoce que la selección sexual es el principal impulsor de la diversidad.
• Además de la comunicación con los miembros del sexo opuesto, los animales sociales tienen que comunicar su atractivo y poder para influir en el comportamiento de los demás. Por la misma razón que en la selección sexual, la señal más generalizada es muestra de baja entropía. Entre todas las especies sociales, los seres humanos han desarrollado la estructura social más compleja. La creación de obras de arte diferentes, la demostración de las proezas atléticas, la acumulación de la riqueza y el consumo conspicuo - todos los cuales representan diferentes formas de baja entropía - son los principales métodos de divulgar la propia atracción.
• A medida que los grupos sociales se hacen más grandes y la división del trabajo más adecuada, las personas se vuelven menos familiarizadas con los demás en sus interacciones diarias, que hace más difícil para las personas juzgar la capacidad de los demás. La necesidad de que las personas divulguen su atractivo gracias a la acumulación externa de baja entropía también se hace más fuerte. La gente suele mostrar su capacidad mediante la compra de viviendas más caras, coches, ropa, ir a restaurantes más caros y asistir a escuelas más exclusivas. El gran esfuerzo que los seres humanos ponen en las actividades no alimentarias reflejan el alto costo de la comunicación en una sociedad enorme y compleja. Las evidencias históricas demuestran que los costes de transacción se han ido incrementando con el tiempo.

Los "costes de transacción" de los que habla Chen significa que la lucha por alcanzar y mantener localizados los estados de baja entropía genera un aumento de la entropía en el universo como un todo.

Preguntas: En su propia vida, ¿cómo experimenta la lucha para lograr y mantener estados de baja entropía? ¿Cuáles son los costes de transacción de esta lucha?, es decir, ¿de qué manera su lucha aumenta la entropía global del mundo? ¿Qué éxito han tenido en sus esfuerzos para lograr y mantener estados de baja entropía? ¿Cómo de sostenibles son esos estados?

Una propiedad sumamente importante de las leyes de Newton es que son de tiempo inverso invariantes. Lo que este término un tanto oscuro quiere decir es que, si la dirección del tiempo se invierte, también se invierten las direcciones de movimiento de todas las partículas, y este movimiento inverso está totalmente permitido por las leyes de Newton. En otras palabras, el movimiento inverso en el tiempo (retroceso) es igual de válido que el movimiento de avance del tiempo, y la misma naturaleza no distingue entre los dos. Un ejemplo simple de esto es el movimiento de tiempo-inverso en el lanzamiento de una pelota de béisbol, que sigue una trayectoria parabólica en ambas direcciones, adelante y atrás o invertida. Si no se ve el acto de lanzar la pelota, y si no hubiera resistencia del viento, nosotros no podríamos distinguir la parábola hacia delante de la parábola invertida. Otra manera de decirlo es que si viéramos una película del lanzamiento de la pelota parecería tan válido para nosotros verla en dirección inversa como en dirección hacia delante. La invariancia del tiempo inverso es también evidente en el movimiento aparentemente aleatorio de las moléculas de un gas. Si pudiéramos ver su movimiento en una película y luego invertirlo, es decir dar marcha atrás a la película, no podríamos distinguir entre el movimiento de avance y el movimiento invertido (ver http://www.colorado.edu/physics/phet/web-pages/simulations-base.html → Heat and Thermo → Gas Properties).

Sin embargo, si consideramos el movimiento de un objeto que contiene muchas partículas ordenadas (por ejemplo, con un tamaño, forma, posición, velocidad y orientación reconocibles), encontramos un fenómeno diferente. Es fácil ver la diferencia entre los movimientos de avance y retroceso (inverso) de una persona, un caballo, una planta creciendo, una taza cayéndose de una mesa y rompiéndose, y muchos otros ejemplos de la vida cotidiana. Otro ejemplo es la libre expansión de un gas que inicialmente está confinado a un lado de una caja por una membrana. Si la membrana se rompe, el gas se extiende inmediatamente al otro lado (inicialmente se asume que se ha evacuado), y podemos distinguir fácilmente el tiempo del movimiento invertido del movimiento de avance. En todos estos casos, el movimiento al nivel de molécula individual es de tiempo inverso invariante, pero está claro que el movimiento bruto del objeto macroscópico no lo es.

Ahora nuestra pregunta es,"¿Por qué la naturaleza parece ser de tiempo inverso invariante al nivel de partícula individual, o unas pocas, pero aparentemente no al nivel de muchas partículas contenidas en un sistema ordenado como cualquier objeto macroscópico común?" En la física clásica, la irreversibilidad siempre se debe a la segunda ley de la termodinámica, que determina la dirección de avance del tiempo. La entropía de un sistema de movimiento de un caballo o persona, fuerza gravitatoria, la tierra, y alrededores aumenta con el tiempo porque el movimiento disipa la energía y aumenta el desorden en el cuerpo, tierra, y alrededores. La dirección hacia delante de una taza cayéndose es evidente después de golpearse contra el suelo y romperse porque la taza rota está más desordenada (tiene una entropía más alta) que la taza no rota. Sin embargo, incluso antes de que la taza se rompa, la entropía del sistema combinado de taza, fuerza gravitatoria y tierra aumenta mientras la taza cae.

Pregunta: ¿Cómo es posible que la entropía de un sistema de taza cayendo, fuerza gravitatoria y tierra aumente incluso antes de que la taza se rompa? Supongamos que la tierra es un conjunto de un gran número de partículas que están en equilibrio térmico en todo momento, es decir, que la energía del movimiento de las mareas es constante y que se transforma en energía térmica.

2.4. Electromagnetismo

El físico francés Charles Augustin de Coulomb (1736-1806) descubrió la ley de la fuerza que obedecían los objetos estacionarios cargados eléctricamente entre 1785 y 1791. En 1820, el físico danés Hans Christian Oersted (1777-1851) descubrió que una corriente eléctrica produce un campo magnético, y que un campo magnético ejercía una fuerza sobre un alambre (cable) de corriente. De 1820 a 1827, el físico francés André Ampere (1775-1836) amplió estos descubrimientos y desarrolló la relación matemática que describe la fuerza del campo magnético como una función de corriente. En 1831, el químico y físico inglés Michael Faraday (1791-1867) descubrió que un campo magnético cambiante, que él explicó desde el punto de vista de las cambiantes líneas de fuerza magnética, produce una corriente eléctrica en un alambre. Éste fue un paso de gigante hacia delante porque fue el precursor del concepto de los campos de fuerza, que se usan actualmente para explicar todas las fuerzas de la naturaleza. Una simulación por ordenador de la fuerza en una carga eléctrica se puede ver en: http://ephysics.physics.ucla.edu/physlets/1.1/e_electric_field.htm.

En 1873, estos distintos fenómenos y teorías fueron todos reunidos en una elegante teoría por el físico escocés James Clerk Maxwell (1831-1879) en 1873. Las cuatro ecuaciones de Maxwell que describen el campo electromagnético son reconocidas como uno de los más grandes logros de la física del siglo 19. Maxwell pudo calcular con sus ecuaciones la velocidad de propagación del campo electromagnético, y descubrió que era aproximadamente igual a la velocidad de luz. Él propuso entonces que la luz es un fenómeno electromagnético. Como los campos electromagnéticos pueden oscilar a cualquier frecuencia, llegó a la conclusión de que la luz visible ocupaba sólo una parte muy pequeña del espectro de frecuencia de la radiación electromagnética. El espectro entero incluye las ondas radiofónicas de baja frecuencia, alta frecuencia, muy alta frecuencia, frecuencia ultra elevada, y microondas. Aún a frecuencias más elevadas están la radiación infrarroja, la luz visible, la radiación ultravioleta, rayos X, y los rayos gamma. Todas éstas son fundamentalmente el mismo tipo de ondas, la única diferencia entre ellas es la frecuencia de radiación (ver la próxima sección).

Ahora nos preguntamos, ¿Qué es el campo electromagnético, a todo esto? ¿Es un objeto físico? Para contestar esa pregunta, debemos entender lo que queremos decir por el término objeto físico. Una definición es que es algo que tiene fuerza, energía y momentum (cantidad de movimiento). Según esta definición el campo electromagnético es un objeto físico porque tiene fuerza, energía, y momento. Sin embargo, esto simplemente define el campo electromagnético en cuanto a otras cosas que requieren sus propias definiciones. La fuerza, la energía y el momentum sólo pueden definirse desde el punto de vista de las operaciones necesarias para medirlos y estas operaciones requieren objetos físicos sobre los cuales hacer las medicións. Por lo tanto, todos los objetos físicos se definen desde el punto de vista de otros objetos físicos, así que la definición es circular. Esta es otra indicación de que el concepto de realidad objetiva no es nada más que un concepto (ver Sección 1.1).

2.5. Las ondas

En los 1800s, se sabía que la luz tenía una naturaleza ondulada, y la física clásica asumió entonces que era una onda. Las ondas son las oscilaciones del desplazamiento. Ejemplos son las ondas del agua que son oscilaciones desplazándose en la superficie del agua; y las ondas de una soga fuertemente estirada, cuando se produce una oscilación de desplazamiento cuando se agita de arriba a abajo. Las ondas se caracterizan por tres parámetros: longitud de onda (λ), frecuencia de oscilación (f), y velocidad (v).

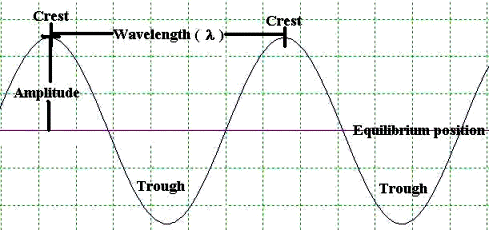
Estos parámetros están relacionados en la ecuación siguiente:

v = λf

El espectro electromagnético (ver la sección anterior) contiene ondas electromagnéticas de todas las frecuencias y longitudes de onda:

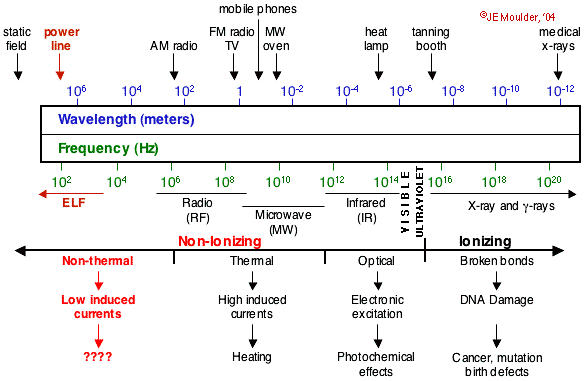
Ver una demostración de las ondas en: http://www.surendranath.org/Applets.html (→ Waves → Transverse Waves) y en: http://www.colorado.edu/physics/2000/index.pl (Table of Contents → Science Trek → Catch the Wave).

No se conocía cuál era la oscilación media en el caso de la luz, pero se dio el nombre de "éter". Maxwell había supuesto que el éter proporcionaba un marco de referencia absoluto en cuanto a que la velocidad de cualquier objeto u onda podría medirse.

En 1881, el físico alemán-americano Albert Michelson (1852-1931) y el físico americano Edward Morley (1828-1923) realizaron experimentos pioneros en la velocidad de luz. Descubrieron que la velocidad de luz en la tierra siempre tenía el mismo valor constante sin tener en cuenta la dirección del movimiento de la tierra alrededor del sol. Esto desobedecía el concepto, que prevalecía en ese momento, de que la velocidad exacta de cualquier objeto, sea partícula u onda, depende de la velocidad del observador en relación con la velocidad del otro objeto. Este concepto se demuestra en la vida cotidiana cuando nuestra observación de la velocidad de otro automóvil depende de la velocidad de nuestro propio automóvil. Por lo tanto, la velocidad exacta de la luz en relación con el éter se suponía que dependía de la dirección del movimiento de la tierra en relación con la velocidad del éter. Pero, la constancia de la velocidad de la luz significaba que el concepto del éter tuvo que ser abandonado porque la velocidad del éter se suponía que no cambiaba con la velocidad del observador de tal manera que la velocidad de la luz siempre tenía el mismo valor. Por consiguiente, en el caso de las ondas de luz, los físicos concluyeron que no hay ningún medio material que oscilara.

Pregunta: De algunos ejemplos de las ondas cuyas velocidades observadas dependen de la velocidad del observador. De algunos ejemplos de las ondas cuyas velocidades observadas no dependen de la velocidad del observador.

2.6. La relatividad

Implícita en la discusión anterior de la física clásica estaba la suposición de que el espacio y el tiempo eran los contextos en que todos los fenómenos físicos tenían lugar. Hasta 1905, los físicos suponían que el tiempo y el espacio eran absolutos en el sentido de que ningún fenómeno físico u observación podrían afectarlos, por consiguiente eran siempre fijos y constantes. Newton pensó que esta hipótesis era necesaria para que sus leyes del movimiento fueran válidas y hasta 1905, ningún físico dudaba de su validez.

En 1905, el físico alemán-suizo-americano Albert Einstein (1879-1955) revolucionó estas ideas del tiempo y el espacio publicando su teoría de la relatividad especial. ("Especial" significa que todos los movimientos son uniformes, es decir, con velocidad constante.) En esta teoría, Einstein abandonó el concepto del éter, y con él el concepto del movimiento absoluto de un objeto, comprendiendo que sólo podía medirse el movimiento relativo entre objetos. Utilizando sólo la suposición de la constancia de la velocidad de la luz en el espacio libre, demostró que ni la longitud ni el tiempo son absolutos. Esto significa que ambas medias de longitud y de tiempo dependen de las velocidades relativas del observador y lo observado.

Un observador que está de pie en el suelo midiendo la longitud de un avión que pasa volando obtendrá un valor minuciosamente más pequeño que el obtenido por un observador en el avión. Un observador en la tierra que comparase un reloj en una nave espacial con un reloj en la tierra verá que el reloj de la nave espacial se mueve más lentamente que el reloj de la tierra. (¡Por supuesto, un observador en la nave espacial verá el reloj de la tierra moviéndose más lentamente que su reloj! Ésta es la famosa paradoja de los gemelos. Se resuelve comprendiendo que, cuando la nave espacial vuelve a la tierra, el observador de la nave espacial y el reloj habrán envejecido menos que el observador de la tierra y e reloj. La diferencia entre los dos observadores es que la nave espacial ha sufrido desaceleración para posarse en la tierra. Esta desaceleración, que es aceleración negativa, es movimiento no-uniforme; por consiguiente la relatividad especial no se aplica.)

Para un objeto que tiene en reposo una masa cero, la teoría especial produjo la famosa relación entre la energía total (E) del objeto, que incluye su energía cinética, y su masa (m):

E = mc²

donde c es la velocidad de la luz en el vacío. La teoría especial de Einstein ha sido confirmada por miles de experimentos, directos e indirectos.

En la teoría de la relatividad especial de Einstein, aunque el espacio y el tiempo ya no eran absolutos, todavía eran euclidianos. Esto significaba que dos líneas rectas en el espacio-tiempo (por ejemplo, en un sistema de coordenadas x,y,z,t) que eran paralelas en un punto siempre permanecían paralelas sin importar las fuerzas gravitatorias.

Preguntas: Supongamos que existe el éter. ¿Cómo afectaría eso a la teoría de la relatividad especial de Einstein? Supongamos que la teoría de la relatividad está equivocada. ¿Cuál sería el efecto en su vida ahora?

En 1915, Einstein completó su mayor trabajo, la teoría general de la relatividad. Mientras que la teoría especial trata de los objetos en movimiento relativo y uniforme, es decir, que se mueven con velocidad constante a lo largo de líneas rectas relativas una a la otra, la teoría general trata de objetos que van acelerando en relación uno con el otro, es decir, que se mueven con velocidades que van cambiando o en trayectorias curvadas. Ejemplos de aceleración de objetos son un avión despegando o aterrizando, un automóvil aumentando o disminuyendo su velocidad, un ascensor que sube o que baja, un automóvil que pasa por una curva a velocidad constante, y la tierra que gira alrededor del sol o la luna que gira alrededor de la tierra a velocidad constante.

Un ejemplo particularmente importante de aceleración es el de un objeto en caída libre por la gravedad de la tierra. Un objeto en caída libre sólo actúa sobre él la fuerza gravitatoria, sin la fricción del aire ni otras fuerzas. Todos los objetos en caída libre en un mismo sitio del campo gravitatorio de la tierra caen con la misma aceleración, independiente de la masa o material del objeto. Un astronauta en una nave espacial, no experimenta la fuerza gravitatoria (es decir, experimenta la ingravidez), por lo tanto podemos decir que la aceleración en caída libre anula la fuerza gravitatoria. Otra manera de expresar este hecho es que una fuerza gravitatoria es equivalente a una aceleración en la misma dirección. Ésta es la célebre equivalencia postulada por Einstein, que él utilizó para descubrir la relatividad general.

La equivalencia postulada se aplica a todos los objetos, incluso a la luz. Por consiguiente, el recorrido de un haz de luz es afectado por un campo gravitatorio igual que la trayectoria de una pelota de béisbol. Sin embargo, debido a la altísima velocidad de los fotones de luz (3x108 metros/segundo, o 300,000 Km./segundo), sus trayectorias están curvadas solamente por cantidades muy diminutas en los campos gravitatorios de objetos ordinarios como el sol.

Como todo tipo de objetos son afectados exactamente de la misma manera por la gravedad, una manera equivalente de ver el problema es reemplazar todas las fuerzas gravitatorias por trayectorias curvadas. ¡Las trayectorias curvadas son entonces equivalentes al mismo espacio curvo! Este es el segundo concepto importante que Einstein utilizó en la teoría general de la relatividad. El resultado es que la teoría general reemplaza el concepto de gravedad por la curvatura del espacio. La curvatura de un rayo de luz alrededor de una estrella individual o una galaxia es muy pequeña y difícil a medir. Incluso el universo entero curvea la trayectoria de un rayo de luz sólo un poquito.

Preguntas: Cerca de la tierra, ¿cómo está el espacio curvado - hacia la tierra, fuera de la tierra, o no lo está? Supongamos que una masa pesada cae más rápido que una masa de menos peso. ¿Cómo afectaría esto a la teoría general de la relatividad de Einstein?

La clara evidencia de que la fuerza de la gravedad no es más que un concepto se demuestra por el hecho de que puede reemplazarse por otro concepto, el concepto de la curvatura del espacio. Está menos claro que las sensaciones del cuerpo que normalmente asociamos con la fuerza de la gravedad (ver Sección 2.2) son también puramente mentales. Veremos más generalmente lo que queremos decir por mente en la Sección 9.2.

La relatividad general también predice la existencia de agujeros negros, objetos que tienen tanta masa pero que son tan pequeños, que el espacio se curva alrededor de ellos. Un haz de luz que se acercara lo suficiente a un agujero negro se curvaría hacia el agujero negro y nunca podría escapar.

Una característica fundamental de la relatividad general es que predice que la materia, la energía, el espacio y el tiempo dependen unos de otros y evolucionan juntos, por lo que el espacio y el tiempo no son magnitudes independientes. Pero, a propósito ¿qué son ellos? ¡De la misma manera que dijimos en la Sección 2.4 que el campo electromagnético no es más que un concepto, y dijimos anteriormente que la gravedad no es más que un concepto, ¡podemos decir ahora también que el espacio no es más que un concepto! El espacio es un concepto que nos permite conceptualizar la separación de los objetos (qué no son más que conceptos) y nos permite predecir las trayectorias de los rayos de luz (qué también no son más que conceptos). El tiempo es un concepto que nos permite conceptualizar cómo cambian los objetos (¡con el tiempo!) Diremos mucho más sobre la conceptualización en la Sección 9.2, y la conceptualización del espacio y el tiempo en el Capítulo 12.

La densidad media de la masa del universo no puede medirse directamente porque somos incapaces de ver la materia que no está emitiendo luz, así que la densidad media de la masa en una galaxia, por ejemplo, debe calcularse de las trayectorias del movimiento de las estrellas visibles de la galaxia. Tales mediciones indican que hay una gran cantidad de materia en el universo que no brilla con su propia o reflejada luz. Esto se llama materia oscura.

En 1929, después de 14 años Einstein publicó su teoría general de la relatividad, el astrónomo estadounidense Edwin Hubble (1889 - 1953) descubrió que el universo se está expandiendo. Hasta 1998, se suponía que la tasa de expansión era constante, pero en 1998 se descubrió que el universo en realidad se está expandiendo a un ritmo creciente en lugar de a uno constante. Esta aceleración no puede explicarse si el universo contiene sólo materia ordinaria y oscura porque éstas producen una fuerza gravitatoria que es atractiva, mientras que una expansión acelerada requiere una fuerza repulsiva. Esta fuerza repulsiva representa una densidad de "energía oscura" además de las densidades de energía de la materia ordinaria y oscura. La materia oscura y la energía oscura están siendo ambas actualmente investigadas intensivamente teórica y experimentalmente porque pudieran ser el resultado del funcionamiento de nuevas leyes físicas.

Hablando del universo como un todo, ¿cuáles son los efectos del espacio curvo? Un efecto importante es que los rayos de luz ya no viajan en línea recta. Por lo tanto, si dos rayos de luz comienzan en paralelo, a la larga o convergen o divergen. Si divergen, se dice que el espacio tiene curvatura negativa, y si convergen, se dice que tiene curvatura positiva. Curvatura cero corresponde a los rayos de luz paralelos que permanecen siempre en paralelo. Esto implica un espacio Euclidiano o plano.

El 11 de febrero de 2003, C.L. Bennett y D.N. Spergel informaron (Science News, 15 de febrero de 2003) sobre un nuevo mapa del comienzo del universo como fue grabado por el satélite WMAP de la NASA. Midiendo las bajísimas temperaturas no-constantes en el trasfondo cósmico de microondas, los investigadores dedujeron que sólo el 4 por ciento del universo es materia ordinaria, mientras que el 23 por ciento es materia oscura fría, y el 73 por ciento es energía oscura. Estos datos, pulidos por las mediciones del quasar en el 2004, indican que el universo es plano y que su edad es de 13.7±0.2 billones de años, la medición más exacta hasta la fecha. Sin embargo, esta estimación de la curvatura depende de la hipótesis de que el universo se está expandiendo a un ritmo constante.

Hay razones teóricas poderosas para creer que la curvatura de nuestro espacio no es positiva ni negativa sino exactamente cero. La curvatura depende de la densidad media de energía (la cantidad promedio de energía por metro cúbico), la tasa de expansión del universo, y la tasa de aumento de la tasa de expansión. En la práctica, es muy difícil medir la curvatura midiendo la curvatura de la trayectoria del rayo de luz, pero se puede estimar si el tamaño medio angular de los puntos de intensidad incide en el fondo cósmico de microondas, la tasa de expansión del universo, y la tasa de aumento en la tasa de expansión, son todas conocidas

(http://www.computerweekly.com/Articles/2009/08/08/237229/The-fate-of-the-cosmos-Dark-energy-can-shape-the-universe.htm).

Nota: En sus documentos iniciales, Einstein había elaborado un modelo del universo con curvatura cero que no se expandía en absoluto. Después, en 1922 pero también antes del descubrimiento de Hubble, el físico ruso Aleksandr Friedmann (1888-1925) descubrió soluciones a las ecuaciones de la relatividad generales que describían un universo en expansión con ambas curvaturas positiva o negativa. Más tarde aún, en 1932 después del descubrimiento de Hubble, Einstein y W. de Sitter elaboraron un modelo que describía un universo en expansión con curvatura cero.

Preguntas: Suponga que no hubiera materia oscura. ¿Cuál sería el resultado observable?
Suponga que no hubiera energía oscura. ¿Cuál sería el resultado observable?

Al inventar la teoría de la relatividad, Einstein fue bastante influenciado por el positivismo del filósofo naturalista austriaco Ernst Mach (1838-1916). El positivismo es la filosofía que establece que el único conocimiento auténtico es el conocimiento científico, basado en la experiencia sensitiva real. Esta actitud se deriva de la creencia de que la única realidad objetiva y externa que existe es la que puede observarse directamente con los sentidos, como los objetos macroscópicos. Al inventar y explicar la teoría especial, Einstein siguió el enfoque positivista e hizo un uso extensivo de las definiciones empíricas de las mediciones del tiempo y el espacio, e incorporó esas definiciones a las matemáticas, que describe cómo varían la longitud y el tiempo con la velocidad relativa del observador y de lo observado. De esta manera, Einstein pudo evitar el concepto del espacio excepto dentro del contexto de las mediciones de longitud y tiempo.

Sin embargo, Einstein abandonó el positivismo cuando desarrolló la teoría general de la relatividad, y es improbable que él pudiera haberla desarrollado sin hacer eso. Su concepto de la relatividad general dependía esencialmente de un salto intuitivo desde los funcionamientos empíricos de medición de la fuerza de gravedad y las aceleraciones de objetos hasta un modelo teórico del espacio que era curvo y en el que no había fuerzas gravitatorias. Él no podría probablemente hacer esto sin creer que el espacio era objetivamente real en lugar de ser simplemente el contexto para hacer mediciones de longitud y tiempo.

Pregunta: Supongamos que la teoría general de la relatividad está equivocada. ¿Cuál sería el efecto en su vida ahora?

Además del espacio curvo, un físico que se adhiriera a la filosofía positivista no habría descubierto el electrón, el átomo, o las ondas cuánticas. El salto intuitivo de Einstein es un ejemplo de un aspecto esencial del trabajo de los científicos. Los experimentos individuales que realizan los científicos son siempre muy específicos a un problema particular en circunstancias particulares. Cualquier esfuerzo por comprender los resultados de muchos de tales experimentos en muchos temas similares sería fútil sin algún tipo de modelo unificador que se supone que representa algún aspecto de la realidad externa objetiva que afecta a esos experimentos. 

Por ejemplo, los campos de fuerza son modelos teóricos de fuerzas gravitatorias o electromagnéticas, y el espacio-tiempo curvo es un modelo de espacio-tiempo que representa la fuerza gravitatoria. Hay otros modelos que representan las fuerzas débiles y fuertes que actúan en las partículas elementales. Y hay modelos del núcleo, el átomo, moléculas, cristales, y gases. Todos estos modelos son muy matemáticos, porque la matemática es el idioma universal de la física.

Cuando se encuentra que un modelo representa con exactitud las observaciones experimentales, hay una fuerte tendencia a pensar en el propio modelo como la realidad externa objetiva. Así, los físicos y el público en general hablan rutinariamente de partículas elementales, núcleos, átomos y espacio-tiempo como si fueran objetos reales, en lugar de simples modelos matemáticos. Veremos después que esta tendencia crea innumerables problemas intentando comprender la verdadera naturaleza de la Realidad.

Pregunta: De su propia experiencia, responda la pregunta, ¿qué es el espacio?

En la física clásica, los objetos interactúan entre sí a través de sus campos de fuerza, que también son objetos en la realidad externa objetiva. Por ejemplo, los átomos y moléculas en un sólido, líquido o gas están unidos por la fuerza electromagnética. Las partículas cargadas también interactúan a través de la fuerza electromagnética. Resulta que todos los objetos físicos, que no son más que conceptos, interactúan entre sí a través de sus campos de fuerza, que también no son más que conceptos (ver Sección 2.4).

Tan revolucionaria como era la teoría general de la relatividad de Einstein, no hizo nada para cambiar la creencia de que nosotros como observadores todavía vivimos dentro del contexto de espacio-tiempo aunque ya no se piensa que el espacio-tiempo es absoluto e inmutable. Esto significa, por ejemplo, que nosotros como objetos todavía estamos sujetos a la experiencia de la separación y el aislamiento de otros objetos, y a la experiencia del envejecimiento y la definitiva muerte del cuerpo. Hizo falta una teoría aún más revolucionaria, la teoría cuántica, para comenzar a agitar estas prisioneras creencias.

Ejercicio: Ver el vídeo de los primeros 15 años de observaciones del primer telescopio Hubble http://imgsrc.hubblesite.org/hu/gallery/db/video/hm_15th_anniversary/formats/hm_15th_anniversary_640x480.mov
¿Qué está viendo el Hubble? ¿Estrellas? ¿Galaxias? ¿El espacio? ¿Un concepto matemático? ¿Consciencia? ¿A nosotros mismos? ¿Nada?

Preguntas: A partir de su propia experiencia, y con el mínimo de conceptos, sea lo más específico y lo más preciso posible al responder las siguientes preguntas. Evite el uso de simples sinónimos. ¿Qué es la fuerza de la gravedad? Un ejemplo de una respuesta inadecuada es "una fuerza que tira de mí hacia abajo y me mantiene en mi silla". En este ejemplo se repite la palabra "fuerza" y se utilizan los conceptos de "tira", "mí", "abajo", "mantiene" "mi " y "silla". Otra respuesta inadecuada es "espacio curvo ", ya que es un sinónimo y no es una experiencia.