Parte 1. La teoría cuántica y la consciencia

4.1. Ondas e interferencia

Revisemos el concepto de la onda de probabilidad. La onda cuántica no aporta energía, momentum, o fuerza. Su única interpretación es que de ella podemos calcular la probabilidad de que una medición dará un resultado particular, por ejemplo, que una película fotográfica medirá una posición específica de un electrón en un haz de electrones, o que un contador de Geiger dará un número específico de rayos gamma de una fuente radiactiva. Es solamente durante una medición que aparece una partícula. Antes de la medición, lo que existe no es algo que pueda ser determinado tanto por la teoría cuántica como mediante un experimento, así que es una pregunta metafísica, no una pregunta de física. Sin embargo, eso no significa que la respuesta metafísica no tenga un considerable impacto tanto en el mundo científico como en el mundo personal de cada uno. Hablaremos mucho más sobre tal consecuencia más tarde.

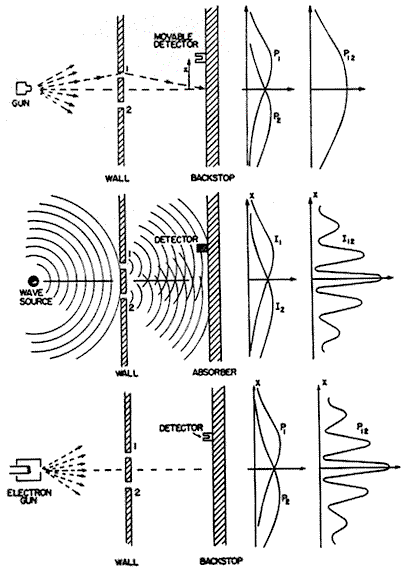
Suponga que hacemos un experimento en que se disparan balas de ametralladora sobre una pared con dos agujeros en ella (ver el diagrama de arriba en la Figura 1). La probabilidad P₁₂ de encontrar una bala que pase por cualquiera de los agujeros incrustada en la pared de contención a la derecha de la pared agujereada es igual a la probabilidad P₁ de encontrar una bala del agujero #1 más la probabilidad P₂ de encontrar una bala del agujero #2. Las distribuciones de probabilidad son sencillamente aditivas.

Cuando tratamos con ondas, tenemos una regla diferente. El principio de superposición es el que cumplen todas las ondas en un medio material siempre que sus amplitudes no sean demasiado grandes, y lo cumplen rigurosamente todas las ondas electromagnéticas y las ondas cuánticas. Este principio establece que la amplitud neta o altura de una onda en cualquier punto en el espacio es igual a la suma algebraica de las alturas de todas las ondas que participan. En el caso de olas (ondas) en el agua, podemos tener olas separadas debido a la estela de un barco, la salpicadura de un nadador, y la fuerza del viento. En cualquier punto de la superficie del agua, las alturas de las olas se suman, pero es importante incluir el signo de la altura que puede ser negativo o positivo. La altura del seno de una ola de agua es negativa mientras que la altura de la cresta es positiva. Cuando una cresta se suma a una cresta, las alturas se suman para dar una cresta más alta, como se muestra abajo. Cuando un seno se suma a una cresta, las alturas tienden a anularse. Exactamente se anulan cuando las alturas de la cresta y el seno son precisamente iguales pero de signo contrario. Cuando un seno se suma a un seno, se crea un seno más hondo. Cuando una cresta no está alineada con una cresta o un seno, se crea una onda intermedia.

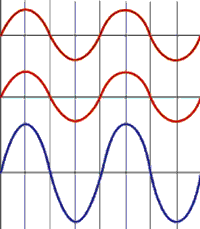
Una cresta sumada a una cresta da una cresta más alta.

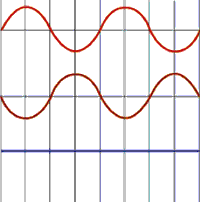
Una cresta sumada a un seno se anulan.

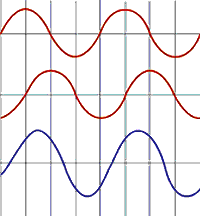
Dos ondas sumadas fuera de fase dan una onda intermedia.

Una animación por ordenador de la superposición de dos ondas puede verse en: http://www.phy.ntnu.edu.tw/ntnujava/viewtopic.php?t=35.

El principio de superposición conduce al fenómeno de interferencia. La superposición, o suma, de dos ondas con la misma longitud de onda en un punto en el espacio donde ambas ondas tienen tanto alturas positivas como negativas producen una onda resultante con una altura positiva o negativa mayor que cualquiera de las dos, como se muestra abajo. Esto se llama interferencia constructiva. Si las alturas individuales tienen signo contrario, la interferencia es destructiva, y la altura de la onda resultante es más pequeña que la altura más grande de las dos.

Mirando hacia abajo una ola en el agua. Las líneas luminosas son las crestas, las oscuras son los senos.

La interferencia de dos olas de agua. Las crestas sumadas a las crestas forman crestas más altas. Los senos sumados a los senos forman senos más hondos.

Una simulación por ordenador de un modelo de interferencia de dos aberturas que utiliza olas de agua se puede ver en: http://www.falstad.com/ripple/, y utilizando ondas de luz en: http://www.walter-fendt.de/ph14e/doubleslit.htm y en: http://www.colorado.edu/physics/2000/index.pl (→ Atomic Lab → Classic Two-Slit Experiment).

Una propiedad mensurable importante de las ondas clásicas es la potencia, o intensidad I (potencia por unidad de área). La potencia es proporcional al cuadrado de la amplitud de la onda, y siempre es positivo. La interferencia de ondas clásicas se ilustra en el gráfico del medio de la Figura 1, dónde la intensidad I₁₂ está trazada en el absorbedor (1). Advierta la diferencia radical entre el gráfico I₁₂ para la ola de agua y el gráfico P₁₂ para las balas. La diferencia es debida a la interferencia. Igualmente, cuando observamos las ondas de luz, también observamos la distribución de la intensidad, no la amplitud de la onda. Una animación por ordenador de la comparación entre las partículas y las ondas en un experimento de dos aberturas se muestra en: http://www.upscale.utoronto.ca/PVB/Harrison/DoubleSlit/Flash/DoubleSlit.html.

Para las ondas cuánticas, nosotros ya sabemos que la propiedad que es proporcional al cuadrado de la amplitud de la onda es la probabilidad. Necesitamos ahora averiguar lo que implica la interferencia para la medición de probabilidades.

Supongamos que ψ₁ y ψ₂ son las amplitudes, o alturas, de dos ondas de probabilidad que representan las partículas indistinguibles medicións en el mismo punto del espacio. (En la teoría cuántica, estas amplitudes son generalmente cantidades complejas. Para simplificar, aquí suponemos que son reales.) La suma de estas dos alturas es simplemente ψ = ψ₁ + ψ₂, así que la probabilidad es

ψ² = (ψ₁ + ψ₂)² = ψ₁² + 2ψ₁ψ₂ + ψ₂²       (Ecuación 1)

Esta ecuación tiene una sencilla interpretación. El primer término de la derecha es simplemente la probabilidad con la que la primera partícula aparecería si no hubiera ninguna interferencia con la segunda partícula, y viceversa para el último término. Por consiguiente estas dos condiciones por sí mismas podrían representar las probabilidades para las partículas clásicas como las balas, a pesar de que normalmente no las representamos por ondas. Si el término del medio no existiera, entonces esta expresión representaría simplemente la suma de estas dos probabilidades clásicas. El diagrama de arriba de la Figura 1, representaría la probabilidad de que una bala pase por el primer agujero o por el segundo y aparece en algún punto particular de la pantalla. La Figura 2 de abajo muestra los impactos de bala propiamente dichos.

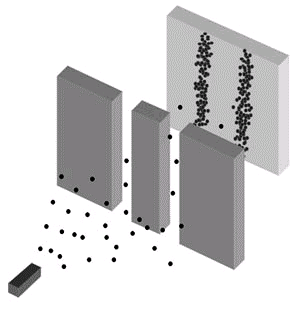
El término del medio en la parte derecha de la Ecuación 1 se denomina término de interferencia. Este término sólo aparece en los fenómenos de onda (incluyendo las ondas clásicas como las olas de agua) y es responsable de la interferencia destructiva o constructiva ya que puede ser negativo o positivo. Si la interferencia destructiva está completa, el término del medio anula completamente los otros dos términos (esto ocurrirá si ψ1 = -ψ2). Debido a la interferencia, las distribuciones de probabilidad de las ondas son completamente diferentes a las de las balas. La distribución de probabilidad de los electrones, marcados P₁₂ en el esquema de abajo de la Figura 1, tiene la misma forma que la distribución de intensidad de las olas del agua mostrada en la figura del medio porque ambas distribuciones se derivan del cuadrado de la suma algebraica de las amplitudes de onda. Los impactos del electrón propiamente dichos se muestran en la Figura 3 de abajo.

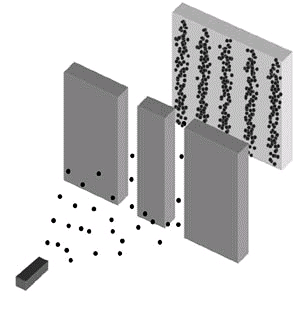
Podemos ahora establecer una importante conclusión de esta discusión. Siempre que observemos la interferencia, hace pensar en la existencia de ondas reales, externas y objetivas en lugar de ondas meramente ficticias que son sólo herramientas para calcular probabilidades de los resultados. Por consiguiente, en este capítulo supondremos que las ondas cuánticas son ondas reales y supondremos por consiguiente que la función de onda es parte de la realidad externa objetiva. Sin embargo, en el Capítulo 6 y después, reexaminaremos esta suposición y propondremos una interpretación sin una realidad objetiva.

Recuerda que cuando detectamos ondas cuánticas, detectamos partículas. Desde que detectamos las partículas, puede parecer que la partícula debe venir de un agujero o del otro, pero eso es incorrecto. Las partículas que detectamos no vienen de los agujeros, aparecen en el momento de la detección. Antes de la detección, tenemos sólo ondas de probabilidad. Una animación por ordenador de un modelo de interferencia de dos aberturas (Experimento de Young) que detecta partículas, ya sean fotones o electrones, puede verse en: http://www.quantum-physics.polytechnique.fr/ (tema 1.1).

¿Qué ocurre cuando intentamos ver que si tenemos electrones a la izquierda de la pantalla de detección, quizás alumbrando con una luz brillante sobre ellos entre los agujeros y la pantalla de detección, y esperamos ver la luz reflejada de estos electrones? Si la luz es bastante intensa como para ver cada electrón de esta manera antes de que sea detectado en la pantalla, elimina el patrón de la interferencia, y solamente vemos la distribución de la partícula clásica mostrada en la figura de arriba. Cualquier medición que manifieste electrones a la izquierda de la pantalla, como cuando se ven bajo una la luz luminosa, elimina la probabilidad de onda que originalmente produjo el patrón de interferencia. Después de esto sólo vemos distribuciones de onda de la probabilidad de la partícula.

4.2. La paradoja del gato de Schrödinger

La idea de este experimento fue creada originalmente por Schrödinger en un intento por mostrar las posibles absurdidades de la teoría cuántica cuando no está limitada exclusivamente a los objetos microscópicos. (Desde entonces, nadie ha tenido éxito en mostrar que la teoría cuántica sea absurda.)

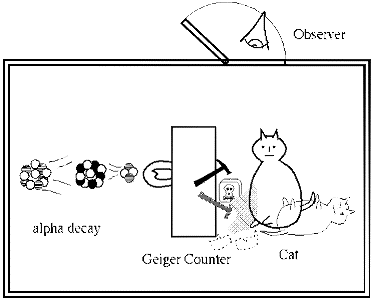
Imaginemos una caja cerrada que contiene un sencillo núcleo radiactivo y un detector de partículas como un contador Geiger (ver el dibujo de arriba). Suponemos que este detector ha sido diseñado para detectar con total seguridad cualquier partícula que sea emitida por el núcleo. El núcleo radiactivo es microscópico y por consiguiente puede definirse por la teoría cuántica. Suponga que la probabilidad de que la fuente emita una partícula en un minuto es ½=50%. El período de un minuto se denomina vida media de la fuente. (Ver la animación de descomposición radiactiva de "Balonium" en: http://www.upscale.utoronto.ca/PVB/Harrison/Flash/Nuclear/Decay/NuclearDecay.html.)

Como la función de onda del núcleo es una solución de la ecuación de Schrödinger y debe describir todas las posibilidades, después de un minuto consiste en una onda con dos términos de igual amplitud, uno corresponde a un núcleo que emite una partícula, y el otro corresponde a un núcleo que no emite ninguna partícula, ambos medidos en el mismo punto del espacio:

ψ = ψ₁ (partícula) + ψ₂ (no partícula)

donde, para simplificar, suponemos de nuevo que las funciones de onda son reales en lugar de complejas. Ahora, ψ₁² es la probabilidad que mostraría una medición donde una partícula fue emitida, y ψ₂² es la probabilidad que mostraría que no fue emitida ninguna partícula. (Veremos abajo que el término de la interferencia 2ψ₁ψ₂ en ψ² no contribuye al resultado final observado.)

Los artículos restantes en la caja son todos macroscópicos, pero como no son más que colecciones de partículas microscópicas (átomos y moléculas) que obedecen la teoría cuántica, suponemos que ellos también obedecen la teoría cuántica

Nota técnica: Si los objetos macroscópicos no obedecen la teoría cuántica, no tenemos ninguna otra teoría para explicarlos. Por ejemplo, la física clásica no puede explicar los siguientes fenómenos macroscópicos y semi-macroscópicos: 1) Franjas de interferencia (Sección 4.1) han sido producidos directamente con buckminsterfulerenos ("buckyesferas")2 que consisten en 60 átomos de carbono y 48 átomos de flúor (C60F48, http://arxiv.org/PS_cache/quant-ph/pdf/0309/0309016v1.pdf). 2) Un dispositivo superconductor de interferencia cuántica (SQUID) que contiene millones de electrones fue hecho para ocupar los estados del gato de Schrödinger (http://www.sciencemag.org/cgi/content/full/287/5462/2395a). 3) Ferromagnetismo, superconductividad, y superfluidad son todos fenómenos cuánticos que ocurren en los sistemas macroscópicos. 4) Se piensa que el período de inflación a principios de la historia del universo fue en su origen la mecánica cuántica (ver las excelentes conferencias sobre cosmología en http://abyss.uoregon.edu/~js/cosmo/lectures.

Por consiguiente, suponemos que el contador Geiger también puede describirse por una función de onda que es una solución para la ecuación de Schrödinger. El sistema combinado de núcleo y detector debe entonces describirse por una función de onda que contiene dos términos, uno que describe un núcleo y un detector que ha detectado una partícula, y otro que describe un núcleo y un detector que no ha detectado una partícula:

ψ = ψ₁ (partícula detectada) + ψ₂ (partícula no detectada)

Los dos términos deben estar presentes necesariamente, y el estado resultante ψ es una superposición de estos dos estados. De nuevo, ψ₁² y ψ₂² son las probabilidades que una medición mostraría cualquier de los dos estados.

Ponemos en la caja una ampolla con gas venenoso y la conectamos al detector para que el gas se libere automáticamente si el detector cuenta una partícula. Ahora ponemos en la caja un gato vivo. Suponemos que el gas venenoso y el gato también pueden describirse por la ecuación de Schrödinger. La función de onda final contiene dos términos, uno que describe una partícula detectada, más la liberación del gas y un gato muerto; y otro que describe una partícula no detectada, más la no liberación del gas y un gato vivo. Ambos términos deben estar presentes si la teoría cuántica puede aplicarse al contenido de la caja. La función de onda debe describir tanto un gato muerto como un gato vivo:

ψ = ψ₁ (partícula detectada, gato muerto) + ψ₂ (partícula no detectada, gato vivo)

Después de un minuto exactamente, miramos dentro de la caja y vemos un gato vivo o uno muerto, ¡pero desde luego no ambos! ¿Cuál es la explicación?

Schrödinger consideró la posibilidad de que ¡mientras no haya observación, no hay ningún gato, ni vivo ni muerto! Sólo hay una función de onda. La función de onda simplemente nos dice qué posibilidades se presentarán al observador cuando la caja se abra. La propia observación manifiesta la realidad de un gato vivo o un gato muerto (esto se llama el observador creó la realidad).

Ahora debemos preguntarnos por qué el propio observador no es incluido en el sistema descrito por la ecuación de Schrödinger, así que lo ponemos en la ecuación siguiente:

ψ = ψ₁ (partícula detectada, el observador ve el gato muerto) + ψ₂ (partícula no detectada, el observador ve el gato vivo)

Si elevamos al cuadrado esta expresión, como en Ecuación 1, obtenemos

ψ² = (ψ₁ + ψ₂)² = ψ₁² + 2ψ₁ψ₂ + ψ₂²

Sabemos que el observador sólo puede observar o un gato vivo o un gato muerto, no una superposición. Eso significa que el término de interferencia de 2ψ₁ψ₂ no contribuye a la observación. ¿Por qué no lo hace? Schrödinger no tienen el beneficio de una amplia investigación teórica realizada en las últimas décadas. Esta ha demostrado que, debido a que en la práctica es imposible aislar un objeto macroscópico de su entorno, debemos incluir sus efectos en esta ecuación. Los efectos ambientales incluyen todas las interacciones entre el resto del universo y todas las coas en el experimento, incluidos el detector, la botella de gas venenoso, el gato, la caja, y el observador. Cuando estos efectos son incluidos y se halla el promedio, sólo queda

ψ² = (ψ₁ + ψ₂)² = ψ₁² + ψ₂²       (Ecuación 2)

Sin el término de interferencia, Ecuación 2 ya no describe la superposición de un gato muerto y un gato vivo. Superficialmente, es similar a la descripción de los objetos clásicos como balas como se mencionó anteriormente la figura. 2. En el caso clásico, antes de una observación el gato es real, pero vivo o muerto. Las probabilidades representan sólo nuestra ignorancia del caso real. Sin embargo, en el caso cuántico, antes de una observación no hay gato, vivo o muerto. Sólo hay una función de onda que representa las posibilidades que se manifestarán cuando se haga una observación.

4.3. El teorema de Bell, los experimentos de Aspect-Gröblacher, y la no-localización de la realidad

Uno de los principios considerado muy sagrado por Einstein y de hecho por la mayoría de los físicos hasta los años ochenta es el principio de causalidad local, o localidad para abreviar. Este principio (que proviene de la teoría de la relatividad especial de Einstein) establece que ningún efecto físico puede transmitirse con una velocidad más rápida que la luz. También está implícito, pero no siempre establecido, el principio de que todos los efectos físicos deben disminuir mientras la distancia entre la fuente del efecto y el objeto aumenta. En la práctica, este principio impide no sólo toda acción-a-distancia instantánea, sino también cualquier acción-a-distancia cuando las distancias son tan grandes que el campo más amplio de fuerza conocido que puede transmitir señales, la fuerza electromagnética, no puede producir el efecto de forma realista. Si se supone que las partículas de un sistema son independientes unas de otras excepto para los efectos físicos que viajan a menor velocidad que la de la luz, se dice que el sistema es local. Esto significa, por ejemplo, que si se hace una medición a una partícula, las otras partículas no pueden ser afectadas antes de que una señal local de la primera partícula pueda alcanzarlas.

Además de la localidad, el otro principio firmemente mantenido era el principio de la realidad objetiva (ver Sección 1.1). Este principio establece que hay una realidad que existe aparte de ser o no observada. Antes del descubrimiento de la mecánica cuántica, esto significaba que esta realidad consistía en partículas u ondas materiales que tenían siempre propiedades físicas definidas, y que podrían conocerse bien mediante una medición o por cálculo utilizando leyes clásicas y un estado inicial conocido. Por ejemplo, una partícula siempre tenía una posición y velocidad definidos antes de la medición, aunque pueda que no hayan sido conocidos hasta que se hizo la medición o el cálculo. Llamamos a esto objetividad fuerte. Después del desarrollo de la mecánica cuántica, aquéllos que creen en una realidad creada por el observador creen que sólo existe una función de onda antes de a una observación pero aún esto se considera que es objetivamente real. Sin embargo, sus parámetros físicos, como la posición y la velocidad, son indefinidos hasta que se hace una medición. Esto se llama objetividad débil.

La objetividad débil era bastante difícil de aceptar por algunos físicos, pero la teoría cuántica predijo algo más que era incluso más difícil de aceptar —que la realidad es no-local. Esto significa que una medición en una partícula en un sistema no-local se correlaciona con una medición en cualquiera de las otras partículas en el sistema aun cuando no pase ninguna señal local de la primera medición a la segunda. Por ejemplo, una medición de la posición de una partícula en un sistema no-local afecta a una medición de la posición en cualquiera de las otras partículas, independiente de cualquiera señales locales. Un sistema no-local de partículas se describe por una función de onda formada por una superposición de funciones de onda de la partícula individual de tal manera que todas las ondas individuales están enganchadas en un todo coherente. En tal superposición coherente, ya no es posible identificar los componentes individuales de la partícula.  El sistema se comporta como un todo en lugar de como una colección de partículas independientes. Describiremos un ejemplo de un sistema no-local cuando hablemos del teorema de Bell más adelante.

Einstein nunca podría aceptar una realidad que fuera no-local o que fuera indefinida. Su ensayo escrito con Podolsky y Rosen en 1935 [la famosa paradoja EPR, ¿Puede Una Descripción Mecánico-Cuántica de la Realidad Física ser Considerada Completa?, A. Einstein, B., Podolsky, N., Rosen, Phys. Rev. 47 (1935) 777-780] fue un intento de usar un 'experimento mental' 3 para mostrar que, como la mecánica cuántica no podría describir una realidad que fuera a la vez local y definida, la teoría estaba incompleta.

Nota biográfica: Este fue el último gran ensayo de Einstein sobre la teoría cuántica. Hasta que él murió en 1955, trato de concebir una "teoría del campo unificado" que uniría la relatividad general y el electromagnetismo en una única teoría. Él fracasó en esto porque no podía aceptar la descripción cuántica del electromagnetismo. En realidad, su fracaso no es mayor que el de los físicos actuales, que han producido muchos candidatos para una teoría del campo unificado pero ninguno que pueda verificarse con las técnicas experimentales actuales.

Siguiendo el ensayo EPR, muchos físicos dedicaron mucho esfuerzo intentando concebir teorías que fueran completas, a saber teorías que asumían que los parámetros como la posición y la velocidad están en todo momento definidos aun cuando sean desconocidos, y que al mismo tiempo daban resultados que están de acuerdo con la teoría cuántica. (Éstas se llaman teorías de variables ocultas que por definición asumen una objetividad fuerte.) Ninguna de estas teorías encontraron una aceptación general porque eran poco elegantes, complicadas, y difíciles de utilizar, y la versión más conocida también resultó ser extremadamente no-local (David Bohm, ver Sección 6.6).

En 1964, John Bell (1928-1990, físico brillante y creativo del Norte de Irlanda) concibió una manera de determinar experimentalmente si la realidad pudiera ser descrita por las teorías de variables ocultas locales, y concibió una desigualdad que sólo era válida si las teorías de variables ocultas locales fueran válidas [On the Einstein Podolsky Rosen Paradox, J.S. Bell, Física 1 (1964) 195-199]. Además, esta desigualdad sólo dependía de cantidades moderadas experimentales, por eso era independiente de cualquier teoría específica. Cualquier violación de la desigualdad demostraría que la realidad no puede ser a la vez fuertemente objetiva y local.

Se hicieron posteriormente muchos experimentos para probar su desigualdad, con el resultado de que siempre se violaba, mostrando así que si hay una realidad fuertemente objetiva, no podría ser local. Además, los experimentos siempre dieron resultados que eran consistentes con las predicciones de la teoría cuántica. Los mejores de estos experimentos fueron hechos por un grupo guiado por el físico francés Alain Aspect en 1981-82 [Realización Experimental de Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: Una Nueva violación de las desigualdades de Bell, Alain Aspect, Phillipe Grangier, Gérard Roger, Phys,. Rev. Lett. 49 (1982) 91-94]. Estos resultados tienen implicaciones de gran repercusión en la interpretación de la teoría cuántica, como veremos más adelante.

Nota: La siguiente discusión es algo técnica. El lector puede desear saltar directamente a las conclusiones en negrita de esta sección.

Los experimentos de Aspect utilizaban pares de fotones, los dos fotones de cada par eran emitidos en direcciones opuestas de una fuente de calcio. Éstos pares de fotones tenían la propiedad de que las direcciones de polarización (direcciones de vibración, que siempre son perpendiculares a la dirección de la propagación) de los dos fotones de un par siempre eran paralelas entre sí, pero las direcciones de polarización de pares diferentes eran distribuidas al azar.

Los dos lados del experimento estaban separados por 12 metros (ver el diagrama de abajo). Cada lado tenía dos detectores, para detectar fotones con dos diferentes direcciones de polarización. Cada detector por separado registraba un número igual de fotones para todas las direcciones de polarización, demostrando que los fotones estaban completamente no-polarizados. Los detectores estaban conectados para medir sólo cómputos coincidentes, es decir, sólo se registraban los fotones si eran detectados aproximada y simultáneamente en A y B. La desigualdad de Bell dice que, si la realidad es local, una cierta función F de éstos cómputos coincidentes, medida para todas las cuatro combinaciones de los dos ángulos de polarización A1, A2 y los dos ángulos de polarización B1, B2, debe estar entre -2.0 y +2.0. Los experimentos arrojaron un valor por Sexpt de 2.70 ± 0.015. Así la desigualdad de Bell fue violada.

Conclusión: El sistema en los primeros experimentos de Aspect era o indefinido o no-local pero no podría haber sido ambos, definido y local. Este resultado era independiente de si era válida o no la teoría cuántica.

Estos experimentos no podían distinguir entre una realidad que no es fuertemente objetiva pero es local; una que es no-local pero fuertemente objetiva; y una que no es fuertemente objetiva ni local. Además, el valor exacto de la función S siempre estaba de acuerdo con las predicciones de la teoría cuántica (S_QM = 2.70 ± 0.05) que asume que los fotones se describen por funciones de onda.

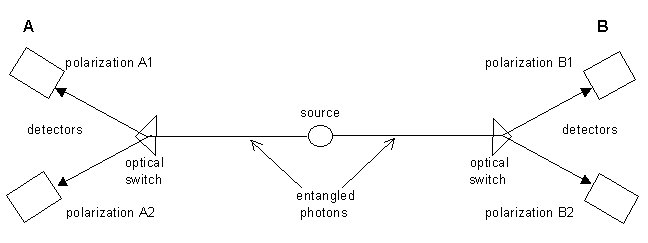
La función F de Bell es una medida de las correlaciones entre las polarizaciones (las direcciones de vibración) medidas en los dos lados A y B.  La existencia de correlaciones no prueba por sí misma que la realidad es indefinida o no-local. De hecho, las correlaciones pueden existir entre medidas en los dos lados ya sea que los fotones son locales y definidos (fotones "reales") o no-locales e indefinidos. Si son locales y definidos, las correlaciones existirán si los dos fotones "reales" emitidos por la fuente son partículas individuales que están polarizadas en paralelo (o perpendicular) unas con otras.  Si son no-locales e indefinidas, las correlaciones pueden existir si el sistema es descrito por una función de onda que es una coherente superposición de las ondas de los dos fotones (un "par enredado"). Como tal función de onda representa un todo coherente en lugar de partículas individuales, permite correlaciones que son mayores que las que pueden existir con fotones locales y definidos. Por eso S es mayor para los fotones enredados o entrelazados que para los fotones locales y definidos, y por eso la medición de la violación de la desigualdad de Bell es consistente con fotones descritos por la teoría cuántica.

Luego, el grupo de Aspect demostró que la violación de la desigualdad de Bell medida en los primeros experimentos no podía deberse a algún tipo desconocido de información de polarización de la señal local de transporte de una serie de detectores hacia otra, en lugar de deberse sólo a las propiedades de las funciones de onda. Por definición, tal señal local habría tenido que propagarse con una velocidad no mayor que la de la luz.  Así, la próxima serie de experimentos fue diseñada para impedir cualquier posible transmisión de la señal local entre los dos lados que afectara los resultados [Experimental test of Bell's inegualities using time-varying analyzers, Alain Aspect, Jean Dalibard, y Gérard Roger, Phys. Rev. Lett. 49 (1982), 1804-1807]. Para hacer esto, la decisión sobre qué dirección de polarización medir en A se tomó después de que una posible señal local de una medición en B estaba ya en tránsito, y lo mismo a la inversa. Por lo tanto, una medición de la polarización en el B no podría afectar a una medición de la polarización en A, y viceversa. La conclusión de la segunda serie de experimentos era que las correlaciones no podrían haber sido un resultado de la señal de transmisión local. Esto implicaba que su sistema era no-local.

Ahora debemos preguntar si cualquier clase de teorías variables ocultas, que son todas diseñadas para ser fuertemente objetivas, pueden excluirse mediante experimento. (El teorema de Bell y los experimentos de Aspect dicen sólo que las teorías variables ocultas deben ser no-locales. Esto no excluye ninguna clase de teoría de variables ocultas no-locales) Para ayudar a contestar esta pregunta, una desigualdad similar a la desigualdad de Bell fue recientemente concebida por Tony Leggett [Nonlocal hidden-variable theories and quantum mechanics: An incompatibility theorem, Foundations of Physics, 33 (2003) 1469–1493]. Se llevó a cabo entonces un experimento por S. Gröblacher y otros para ver si una amplia clase de teorías variables ocultas (que son todas no-locales) podían excluirse [An experimental test of non-local realism, Nature 446 (2007) 871-875].  

Gröblacher y otros concluyeron que ninguna teoría de variables ocultas que no es 'contra-intuitiva' (que no es extraña) puede describir la realidad. Si así fuera, entonces la realidad no puede tener las propiedades definidas antes de la medición. Los experimentos de Aspect y Gröblacher tomados en conjunto dan a entender firmemente que la realidad es indefinida y no-local (no hay partículas "reales"). Esta conclusión es independiente de si la teoría cuántica es válida o no.

Los experimentos de Aspect y Gröblacher y otros no demuestran que la teoría cuántica sea válida pero es consistente con sus predicciones. [Ninguna cantidad de experimentos puede demostrar que cualquier teoría física sea válida. Sin embargo, basta con un solo experimento bien hecho, si es confirmado independientemente por investigadores independientes, para demostrar que una teoría física no es válida.] Hemos visto en la Sección 3.2 que, si la teoría cuántica es válida, no nos dice lo que hay allí antes de una medición. Ésta es la propiedad de la indefinidad. En el Capítulo 6 veremos también que la teoría cuántica es no-local.

En un sistema no-local, una medición hecha en un extremo del sistema está correlacionada con una medición hecha en el otro extremo aun cuando no pase ninguna señal entre los dos. Podría pensarse que, como las correlaciones no-locales pueden existir entre eventos que ocurren en dos puntos diferentes, los observadores en estos dos puntos podrían utilizar estas correlaciones para comunicarse instantáneamente entre sí en la violación de la teoría especial de la relatividad de Einstein. Sin embargo, la no-localidad de la teoría cuántica implica una correlación entre conjuntos de datos, no una transmisión de información a velocidades mayores que la luz. Así, la teoría especial no es violada.  Podemos ver esto dándonos cuenta que los fotones detectados tanto en A o B ocurre completamente al azar tanto en el tiempo como en la polarización. Por consiguiente, el observador A no ve la información en sus datos solo, e igualmente con el observador B. Es solamente después comparando estos conjuntos de datos aleatorios que puede descubrirse una correlación entre los dos conjuntos. 

Nota técnica: Los cálculos teóricos indican que el ojo humano puede ser lo suficientemente sensible para detectar la correlación de pares de fotones sin la ayuda de dispositivos electrónicos, Possible entanglement detection with the naked eye, Brunner, Branciard, Gisin, Phys.. Rev. A 78 (2008) 052110.

Pueden haber fuertes correlaciones entre dos conjuntos aleatorios que no pueden descubrirse mirando un conjunto solo. Esto es ilustrado por el ejemplo de las estereografías aleatorias (los diagramas del Ojo Mágico, ver www.magiceye.com abajo) que, al primer vistazo, se parecen a patrones casi aleatorios de puntos coloreados (ver abajo). Sin embargo, en realidad hay presentes dos patrones casi aleatorios separados, y son desplazados uno de otro por una distancia aproximadamente igual al espacio entre los ojos de una persona. Así, mirando el patrón con los ojos en dirección no convergente como si miráramos a lo lejos, los dos ojos ven patrones diferentes. Las correlaciones entre los patrones son percibidas por el cerebro, y se ve una imagen tridimensional.

Las imágenes del Ojo Mágico pueden verse fácilmente si se ven sobre el papel en lugar de en la pantalla del ordenador. Si es posible, imprima esta imagen y siga las instrucciones debajo. (No necesita imprimir en color.)

Sostenga el centro de la imagen impresa cerca de su nariz. Se verá borrosa. Enfoque la mirada como si estuviera mirando a través de la imagen en la distancia. Muy despacio mueva la imagen fuera de su cara hasta que los dos cuadrados sobre la imagen se conviertan en tres cuadrados. Si usted ve cuatro cuadrados, mueva la imagen más lejos de la cara hasta que usted vea sólo tres cuadrados. ¡Si usted ve uno o dos cuadrados, vuelva a empezar!

Cuando vea tres cuadrados claramente, mantenga la página un momento y la imagen oculta aparecerá mágicamente. Una vez que percibe la imagen oculta y el fondo, puede ver la imagen entera en 3D. Cuanto más tiempo la mire más clara se percibe la ilusión. Cuanto más lejos mantenga la página, más profunda se vuelve. ¡Buena Suerte!

4.4. Otra violación experimental de la teoría del observador independiente.

En la Sección 4.3 se habló de los conflictos entre las variables ocultas y las descripciones cuánticas de los experimentos que se hicieron en los objetos cuánticos enredados o entrelazados, como los pares de fotones enredados. Recientemente, se han realizado mediciones en pares de iones atrapados que estaban enredados, e incluso con estas partículas no enredadas, los resultados fueron consistentes con la teoría cuántica, pero incompatibles con la hipótesis de observadores independientes de partículas (State-independent experimental test of quantum contextuality, Kirchmair, Zähringer, Gerritsma, Kleinmann, Gühne Cabello, Blatt, Roos, Nature 460 (2009), 494-497).