Parte 1. La teoría cuántica y la consciencia
Capítulo 3. La física cuántica desde Planck y Einstein a Bohr, Heisenberg, de Broglie, y Schrödinger
3.1. El comienzo de la física cuántica de Planck y Einstein
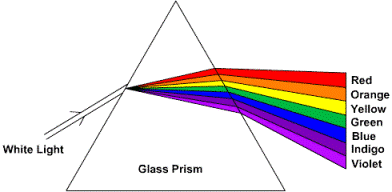
Los físicos miden el espectro (la intensidad de la luz como una función de longitud de onda, o color) de una fuente de luz en un espectrómetro. La figura de abajo muestra un dibujo esquemático de un simple espectrómetro de prisma. La luz blanca entra por la izquierda y el prisma dispersa la luz en los colores del espectro.
A finales de 1800, los físicos hacían mediciones exactas del espectro de las emisiones de los cuerpos negros (objetos que son opacos, o muy absorbentes, de la luz que emiten). Buenos ejemplos de cuerpos negros son el sol, el filamento de una lámpara incandescente, y el quemador de una estufa eléctrica. El color de un cuerpo negro depende de su temperatura, un cuerpo frío que emite radiación de longitudes de onda larga, es decir, en la escala de frecuencias de radio o en el infrarrojo que es invisible al ojo, un cuerpo más caliente que emite radiación que incluye longitudes de onda más cortas y que aparece de color rojo intenso, un cuerpo aún más caliente que emite una radiación que incluye aún longitudes de onda más cortas y aparece de color amarillo, y un cuerpo caliente que emite longitudes de onda aun más cortas y aparece de color blanco. Las emisiones siempre están por encima de una amplia gama de colores, o longitudes de onda, y su apariencia es el resultado neto de ver todo los colores a la vez. Ejemplos de varios espectros de un cuerpo negro se muestran abajo. Las simulaciones por ordenador pueden verse en: http://ephysics.physics.ucla.edu/physlets/eblackbody.htm.
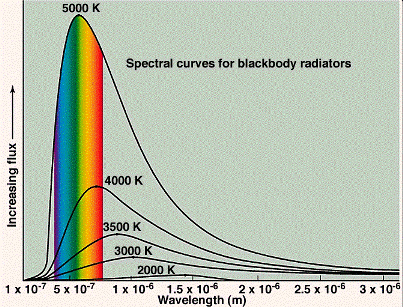
Pregunta: Según la definición anterior, ¿Es tu cuerpo un cuerpo negro? Nota: El cuerpo humano puede verse en la oscuridad con gafas térmicas.
La física clásica no podría explicar los espectros de los cuerpos negros. Se prevé que la intensidad (el poder que emite una cierta longitud de onda) de la luz emitida debe aumentar rápidamente con la decreciente longitud de onda sin límite (la "catástrofe ultravioleta"). En la figura de abajo, la curva llamada "ley Rayleigh-Jeans" muestra la conducta clásica que se esperada.
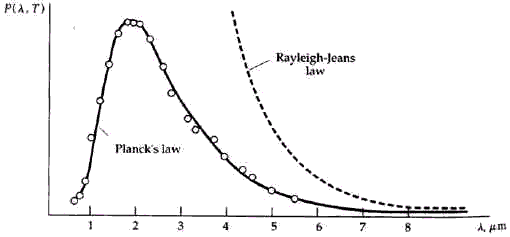
Sin embargo, las mediciones de los espectros mostraron realmente una intensidad máxima en una longitud de onda particular, mientras que la intensidad disminuyó en las longitudes de onda por encima y por debajo del máximo. Para explicar los espectros, en 1900 el físico alemán Max Planck (1858 - 1947) se vio forzado a hacer una desesperada suposición para la cual él no tenía ninguna explicación física. Como con la física clásica, él supuso que el cuerpo consistía de osciladores vibrantes (qué realmente eran colecciones de átomos o moléculas). Sin embargo, en contraste con la física clásica, que supone que cada oscilador podría absorber una cantidad arbitraria de energía de la radiación o emitir una cantidad arbitraria de energía hacia él, Planck se vio forzado a suponer que cada oscilador podría recibir o emitir sólo energías discretas cuantizadas (E), tal como
E = hf (Fórmula de Planck)
donde h (la constante de Planck) es un número sumamente pequeño cuyo valor no necesitamos aquí, y f es la frecuencia vibratoria del oscilador (el número de veces que vibra por segundo). Se asume que cada oscilador sólo vibra a una frecuencia fija (aunque con osciladores diferentes en general se obtenían frecuencias diferentes), así que si emitiera alguna radiación, perdería igual de energía que hf, y si absorbiera alguna radiación, ganaría igual de energía que hf. Planck no entendía cómo podría ser esto, él solamente hizo esta suposición empírica para explicar los espectros. La figura de arriba muestra la predicción de Planck; esto estaba de acuerdo con las mediciones de los espectros.
También en a finales de 1800, físicos experimentales estaban midiendo la emisión de electrones de los objetos metálicos cuando se proyectaba una luz sobre el objeto. Esto se llamó el efecto fotoeléctrico. Estos experimentos que usan los conceptos clásicos tampoco podrían explicarse. Estos físicos observaron que esa emisión de electrones sólo ocurría para longitudes de onda de luz más cortas que cierto valor mínimo que dependía del metal. Clásicamente, sin embargo, uno espera que la emisión no debiera depender en absoluto de la longitud de onda, sino sólo de la intensidad, con intensidades mayores que producen mayores emisiones de electrones. Una simulación por ordenador del efecto fotoeléctrico se puede ver en http://phet.colorado.edu/simulations/sims.php?sim=Photoelectric_Effect (→ Quantum Phenomena → Photoelectric Effect). El diagrama de abajo ilustra el efecto.
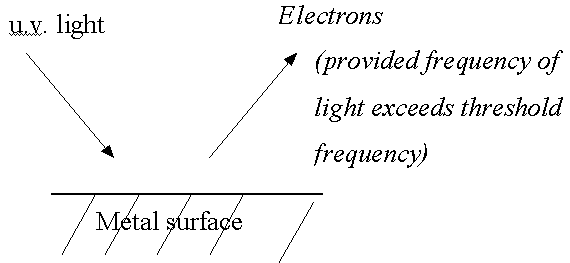
En una de una serie famosa de ponencias en 1905, Einstein explicó el efecto fotoeléctrico empezando con el concepto de Planck de los intercambios de la energía cuantizada con la radiación de la luz, y elaboró la sorprendente suposición de que estos intercambios cuantizados eran resultado directo de la misma cuantización de la luz, es decir la luz consistía en discretos paquetes (cuantos) de energía llamados fotones, en lugar de ondas continuas que siempre habían supuesto los físicos clásicos. Sin embargo, estos paquetes aún tenían una naturaleza de onda, y podrían caracterizarse por una longitud de onda que determinaba su color. Él también utilizó la relación de Planck entre la energía y la frecuencia (E = hf) para identificar la energía del fotón, y usó la relación entre la velocidad, frecuencia y longitud de onda que la física clásica siempre habían usado (v=λf, dónde ahora v=c = velocidad de la luz). Einstein recibió el Premio Nobel por esta ponencia (¡no por sus teorías de la relatividad!).
En la física clásica, el campo electromagnético conecta las partículas cargadas unas con otras (ver Secciones 2.4, 2.6). En la física cuántica, los campos de fuerza de la física clásica están cuantizados, y los cuantos de los campos entonces se convierten en portadores de fuerza. Por ejemplo, los fotones son los cuantos del campo electromagnético. En la física cuántica, son los fotones los que conectan las partículas cargadas unas con otras.
3.2. El desarrollo de la mecánica cuántica de Bohr, Heisenberg, de Broglie y Schrödinger
Además de medir los espectros de la radiación de los cuerpos negros en el siglo 19, los físicos experimentales también estaban familiarizados con los espectros que emitían los gases a través de los cuales pasaba una descarga eléctrica (una corriente eléctrica con bastante energía como para deshacer algunos de los electrones de los átomos del gas). Ejemplos de tales descargas son las familiares señales de neón en las que el gas es el neón; y la lámpara fluorescente en donde el gas es vapor de mercurio (la lámpara fluorescente tiene capas especiales en las paredes internas que cambian el espectro de la luz). Los espectros de tales fuentes de luz consisten en emisiones a longitudes de onda discretas separadas, en lugar de sobre una banda continua de longitudes de onda como en los espectros de los cuerpos negros. Estos espectros se llaman espectros de línea debido a su apariencia cuando se ven con un espectrómetro (ver Sección 3.1 y figura de abajo). Puede verse una simulación (applet) por ordenador de espectros de línea en: http://jersey.uoregon.edu/vlab/elements/Elements.html.
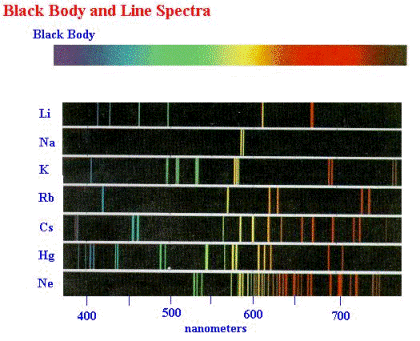
Los espectros de línea son otro ejemplo de fenómenos que no podrían explicarse por la física clásica. De hecho, la explicación no podría venir hasta que los desarrollos en la comprensión de la estructura atómica hayan sido elaborados por el físico neozelandés Ernest Rutherford (1871-1937) y sus colaboradores en 1911. Dispersando las partículas alfa (es decir, núcleos de helio que consisten en dos protones y dos neutrones unidos) de laminas delgadas de oro, descubrieron que el átomo de oro estaba compuesto de un diminuto núcleo (10-15 metros) muy denso, cargado positivamente y rodeado por una nube mucho más grande (10-10 metros) de electrones cargados negativamente, ver la figura de abajo. (Según la mecánica cuántica, esta imagen no es correcta, pero por ahora es adecuada.)
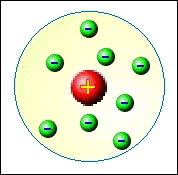
Cuando se aplicó la física clásica a este modelo de átomo, se predijo que los electrones no podían permanecer en órbitas estables alrededor del núcleo, sino que radiarían toda su energía y caerían dentro del núcleo, igual que un satélite cae a la tierra cuando pierde su energía cinética debido a la fricción atmosférica. En 1913, después de que el físico danés Niels Bohr (1885-1962) había aprendido de estos resultados, construyó un modelo de átomo que aprovechaba las ideas cuánticas de Planck y Einstein. Él propuso que los electrones ocupaban órbitas discretas estables sin radiar su energía. La discreción era resultado de la cuantización de las órbitas, en donde cada órbita corresponde a un electrón con una específica energía cuantizada. Se requería que el electrón tuviera un cierto cuanto de energía mínimo correspondiente a una órbita más pequeña; así, las reglas cuánticas no permitían al electrón caer dentro del núcleo. Sin embargo, un electrón podría saltar de una órbita superior a una inferior y emitir un fotón en el proceso. La energía del fotón podría asumir sólo el valor que corresponde a la diferencia entre la energía del electrón en las orbitas superiores e inferiores. Un electrón también podría absorber un fotón y saltar de una órbita inferior a una superior si la energía del fotón es igual a la diferencia entre las energías de la órbita, ver la figura de abajo. Las animaciones por ordenador del modelo de Bohr de la emisión de fotón y la absorción en el átomo de hidrógeno se pueden ver en: http://www.upscale.utoronto.ca/PVB/Harrison/BohrModel/Flash/BohrModel.html y http://www.colorado.edu/physics/2000/index.pl (Table of Contents → Science Trek Applets → Bohr's Atom).
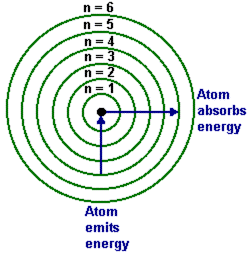
Bohr aplicó su teoría al átomo más simple, el átomo de hidrógeno que está compuesto de un electrón que orbita alrededor del núcleo de un protón. La teoría explicaba muchas de las propiedades del espectro de línea del hidrógeno observado, pero no podía explicar el próximo átomo más complicado, el de helio, que tiene dos electrones. No obstante, la teoría contenía la idea básica de las órbitas cuantizadas, que se conservaron en las teorías más correctas que vinieron después.
En los primeros días del desarrollo de la teoría cuántica, los físicos, como Bohr, intentaron crear representaciones físicas del átomo de la misma manera que ellos siempre habían creado las representaciones físicas en la física clásica. Sin embargo, aunque Bohr desarrolló su modelo inicial del átomo de hidrógeno usando un modelo fácilmente visualizado, tenía características que no se entendían, y no podía explicar el átomo más complicado de dos electrones. Los grandes avances teóricos vinieron cuando algunos físicos alemanes que eran matemáticamente muy sofisticados, Werner Heisenberg (1901-1976), Max Born (1882-1970) y Pascual Jordan (1902-1980), en gran parte habían abandonado las representaciones físicas y creado teorías completamente matemáticas que explicaban las características detalladas del espectro del hidrógeno desde el punto de vista de los niveles de energía y las intensidades de las transiciones radiactivas de un nivel a otro. La característica fundamental de estas teorías era el uso de matrices en lugar de números ordinarios para describir las cantidades físicas como la energía, la posición, y el momentum. (Una matriz es una serie de números que obedecen reglas de multiplicación que son diferente de las reglas que obedecen los números.)
Nota biográfica: Durante la Segunda Guerra Mundial, Heisenberg trabajó en el proyecto alemán de energía nuclear. Si su papel en el proyecto era puramente científico o si había motivos políticos, o si trabajaba para tener éxito o para su fracaso, sigue siendo motivo de controversia. No existe tal controversia sobre el papel de Jordan, quien se unió al partido nazi como guardia de asalto en 1933, y a la Luftwaffe en 1939 como analista del tiempo. Nacido, por el contrario, después de haber sido clasificado como Judio por los nazis en 1933, abandonó Alemania y tomó un puesto en la Universidad de Cambridge, regresando a Alemania sólo después de la guerra.
El paso de recurrir a teorías completamente matemáticas que no están basadas en representaciones físicas fue un cambio radical en los primeros días de la teoría cuántica, pero hoy con el desarrollo de las teorías de partículas elementales es una práctica normal. Tales teorías llegan a ser tan arcanas que las representaciones físicas se han vuelto difíciles de crear y representar, y son normalmente desarrolladas para ajustarse a las matemáticas en lugar de ajustarse las matemáticas a la representación. Por lo tanto, adoptando una filosofía positivista impedirían el progreso en los modelos de la realidad en desarrollo, y los modelos que se intuyen son más matemáticos que físicos.
No obstante, en los primeros años de la década de 1920 algunos físicos continuaron pensando en función de la física en lugar de los modelos matemáticos. En 1923, el físico francés Louis de Broglie (1892-1987) razonó que si la luz podría comportarse como las partículas, entonces las partículas como los electrones podrían comportarse como las ondas, y dedujo la fórmula de la longitud de onda de las ondas:
λ = h/p
donde p es el momentum (masa x velocidad) del electrón. Los experimentos posteriormente verificaron que los electrones realmente se comportan como ondas en experimentos que son diseñados para revelar la naturaleza de la onda. Nosotros diremos más sobre estos experimentos en el Capítulo 4. Una demostración por ordenador de de las ondas de Broglie se puede ver en: http://www.colorado.edu/physics/2000/index.pl (Table of Contents → Atomic Lab → Science Trek → de Broglie's atom).
En la física, si hay una onda entonces debe haber una ecuación que describe cómo la onda se propaga en el tiempo. De Broglie no la encontró, pero en 1926 el físico austriaco-irlandés Erwin Schrödinger (1887-1961) descubrió la famosa ecuación que lleva su nombre. La ecuación de Schrödinger nos permite calcular con precisión la onda de Schrödinger en todos los puntos del espacio en cualquier momento futuro si conocemos la onda en todos los puntos del espacio en algún momento inicial. Incluso en este sentido, la teoría cuántica es completamente determinista.
Schrödinger verificó su ecuación usándola para calcular el espectro de emisión de línea del hidrógeno, que él podía hacer sin entender realmente la importancia de las ondas. De hecho, Schrödinger interpretó mal las ondas y pensó que representaban a los propios electrones, ver figura de abajo. Sin embargo, tal interpretación no podría explicar por qué los experimentos siempre mostraban que los fotones emitidos por un átomo eran emitidos al azar en lugar de en momentos predecibles, aunque la proporción media de emisión pudiera predecirse de las teorías de Heisenberg y Schrödinger. Tampoco podría explicar por qué, cuando un electrón es detectado, siempre tiene una posición bien definida en el espacio, en lugar de estar disperso por el espacio como una onda.
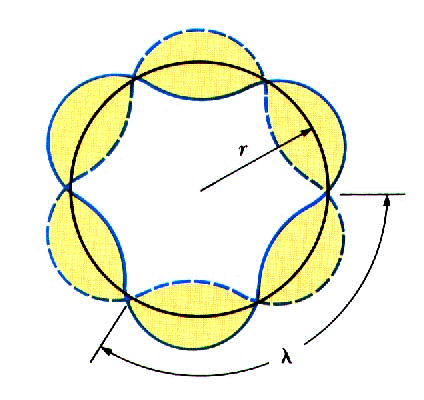
La interpretación adecuada fue descubierta por el físico alemán Max Born (1882-1970) en 1926, quién sugirió que la onda (en realidad el valor absoluto elevado al cuadrado de la amplitud o altura de la onda, en un punto en el espacio) representa la probabilidad de que el electrón aparecerá en ese especificó punto en el espacio si un experimento se hace para medir la posición del electrón. Por lo tanto, la onda de Schrödinger es una onda de probabilidad, no una onda que tiene fuerza, energía y momento como la onda electromagnética. La interpretación de Born introduce dos características sumamente importantes de la mecánica cuántica:
- De la onda, sólo podemos calcular probabilidades, no certezas (la teoría es probabilística, no determinista).
- La onda sólo nos informa de la probabilidad de encontrar algo si miramos, no de lo que hay si no miramos. La teoría cuántica no es una teoría sobre la materia real objetiva (aunque Born pensó que la onda de Schrödinger era objetivamente real).
La primera característica desobedece la segunda suposición fundamental de la física clásica (ver Sección 2.2), es decir, que la posición y la velocidad de un objeto pueden medirse sin límites en su precisión excepto los de los instrumentos de medición. La segunda característica desobedece la primera suposición fundamental de la física clásica, es decir, que el mundo objetivo existe independientemente de cualquier observación que se haga de él.
Preguntas: Suponga que acepta el principio de que la realidad es probabilística en lugar de determinista. ¿Cómo afectaría a su concepto del libre albedrío? ¿Cómo afectaría a su sentido de control sobre sus pensamientos, sentimientos, decisiones y acciones? ¿Cómo afectaría a sus percepciones el control de las personas sobre sus pensamientos, sentimientos, decisiones y acciones? ¿Cómo afectaría a sus juicios sobre usted y los demás?
3.3. Un ejemplo claro de la probabilidad de medición
Las probabilidades pueden medirse utilizando instrumentos sofisticados. Un ejemplo claro se muestra en el diagrama siguiente, medido con un microscopio de efecto túnel, de las probabilidades de las localizaciones de 48 átomos de hierro que circulan alrededor de las probabilidades de la localización de un mar de electrones (http://picasaweb.google.com/IBMResearchAlmaden/IBMCelebrates20YearsOfMovingAtoms#5385522009881657778):
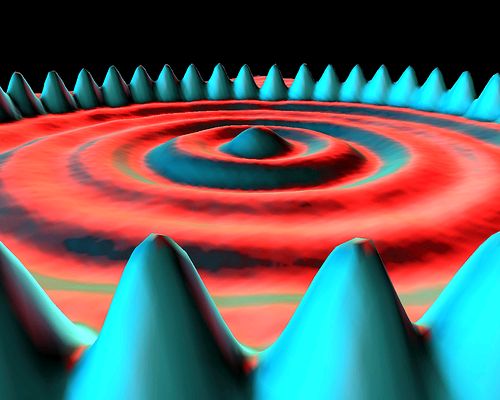
Los términos "átomo de hierro" y "electrón" son intentos heurísticos para dar nombres a las localidades. Sin embargo, este diagrama de ninguna manera demuestra que en realidad hay cosas tales como átomos de hierro y electrones. No hay forma de demostrar eso (ver Sección 1.1), pero, al darle nombres, tendemos a estar convencidos de que los objetos realmente existen.
Las mediciones de probabilidad están representadas por puntos tan densos que parece que forman superficies en lugar de mediciones individuales. Los "átomos de hierro" se consideran muy probablemente localizados bajo los picos de color azul, mientras que los "electrones" se consideran localizados de forma más difusa en los anillos circulares. Estas son mediciones de probabilidad de localizaciones solamente, no lugares reales.
3.4. Incertidumbre y complementariedad
Como propuso Born, la teoría cuántica es intrínsecamente probabilística en tanto que en la mayoría de los casos no puede predecir los resultados de las observaciones individuales. Sin embargo, es determinista en tanto que puede predecir exactamente las probabilidades que se obtendrán de los resultados específicos. Otra manera de decir esto es que puede predecir exactamente los valores medios de las cantidades medicións, como la posición, velocidad, energía, o número de electrones detectados por unidad de tiempo en un haz de electrones, cuando se han hecho un gran número de mediciones en haces de electrones idénticos. No puede predecir los resultados de una sola medición. Esta aleatoriedad no es un fallo de la teoría —es una propiedad intrínseca de la naturaleza. La naturaleza no es determinista en cuanto a lo que se piensa en la física clásica.
Otra característica del mundo cuántico, el mundo de los objetos microscópicos, es que es intrínsecamente imposible calcular simultáneamente la posición exacta y el momentum de una partícula. Éste es el célebre principio de incertidumbre (o de indeterminación) de Heisenberg, que se obtiene utilizando las reglas de la multiplicación para matrices que él usó para la posición y el momentum. Por ejemplo, un aparato diseñado para medir la posición de un electrón con cierta exactitud se muestra en el diagrama siguiente. El agujero en la pared garantiza que las posiciones de los electrones cuando atraviesan el agujero están dentro del agujero, no fuera de él.
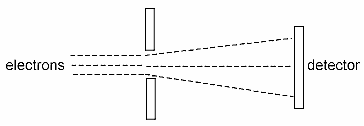
Hasta ahora, esto no es diferente de la física clásica. Sin embargo, la teoría cuántica dice que si conocemos la posición q del electrón dentro de una precisión Δq (diámetro del agujero), entonces nuestro conocimiento del momentum p (= masa x velocidad) en ese punto está limitado a una precisión Δp tal que
(Δp) (Δq)>h (relación de incertidumbre de Heisenberg)
En otras palabras, cuanto más conocemos con exactitud la posición del electrón (menor es Δq), menos conocemos con exactitud el momentum (mayor es Δp). Puesto que el momentum (la cantidad de movimiento) es la masa multiplicada por la velocidad, la incertidumbre del momentum es equivalente a una incertidumbre en la velocidad. La incertidumbre en la velocidad está en la misma dirección que la incertidumbre en la posición. En el dibujo de arriba, la incertidumbre en la posición es una incertidumbre vertical. Esto significa que la incertidumbre en la velocidad también es una incertidumbre vertical. Esto se representa por las líneas divergentes (por una cantidad incierta) después de que los electrones salen del agujero (posición vertical incierta) en lugar de permanecer paralelos como lo están a la izquierda.
Igualmente, un experimento diseñado para medir el momentum con cierta exactitud no podrá localizar la posición de la partícula con mejor exactitud que lo permite la relación de incertidumbre.
Hay que advertir que en la relación de incertidumbre, si el lado derecho es igual a cero, entonces Δp y Δq también pueden ambos ser cero. Ésta es la suposición de la física clásica, que dice que si las partículas siguen trayectorias paralelas en la parte izquierda, no serán perturbadas por el agujero, y seguirán trayectorias paralelas en la parte derecha.
Si dividimos ambos lados de la relación de incertidumbre por la masa m de la partícula, obtenemos
(Δv)(Δq)>h/m
Aquí vemos que las incertidumbres en la velocidad v o posición q son inversamente proporcionales a la masa de la partícula. Por eso una manera eficaz de hacer el lado derecho cero es hacer la masa muy grande. Cuando se ponen los números en esta relación, resulta que las incertidumbres son importantes cuando la masa es microscópica, pero para una masa macroscópica la incertidumbre es imperceptiblemente pequeña. Por lo tanto, la física clásica, que siempre trata con objetos macroscópicos, estaba cerca de ser correcta al asumir que la posición y la velocidad de todos los objetos pudieran determinarse arbitrariamente con precisión.
El principio de incertidumbre puede explicarse en una representación de onda. Una onda con un momentum determinado con precisión corresponde a una infinitamente larga sucesión de ondas, todas con la misma longitud de onda, como se muestra en el primero de los dos patrones de onda de abajo. Esta onda se propaga por todo el espacio, así que su ubicación es indeterminada.
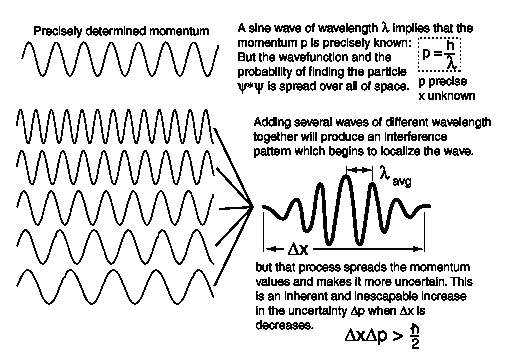
Una onda con un momentum determinado de menos precisión puede obtenerse superponiendo juntas (ver Sección 4.1) las ondas con longitud de onda ligeramente diferente (y por consiguiente con momentum ligeramente diferente), como se muestra arriba en el segundo de los dos patrones. Esto resulta en un paquete de ondas con un momentum extendido Δp (incertidumbre Δp), pero que se agrupan juntas en una región de anchura Δx (incertidumbre Δx) en lugar de extenderse por todo el espacio.
La relación de incertidumbre se relaciona estrechamente con el principio de complementariedad que fue primero enunciado por Bohr. Este principio establece que los objetos cuánticos (objetos representados por funciones de onda cuántica) tienen una naturaleza tanto de partículas como de ondas, y un intento por medir con precisión una propiedad de partícula tenderá a dejar indefinida la propiedad de onda, mientras que un intento por medir una propiedad de onda con precisión tenderá a dejar indefinida la propiedad de partícula. En otras palabras, las propiedades de partícula y las propiedades de onda son propiedades complementarias. Ejemplos de propiedades de partícula son el momentum y la posición. Ejemplos de propiedades de onda son la longitud de onda y la frecuencia. Una medición precisa del momentum o la posición deja indefinida a la longitud de onda o frecuencia, y una medición precisa de la longitud de onda o frecuencia deja indefinido al momentum o posición.
Pregunta: Supongamos que el principio de complementariedad se extiende a los objetos macroscópicos. Por ejemplo, si su intención es ver una ola de agua, se ve una ola de agua, pero no una partícula de agua. Si su intención es ver una partícula de agua, se ve una partícula de agua, pero no una ola de agua. En otras palabras, sólo se ve lo que se quiere ver. ¿Puede pensar en ejemplos similares de este principio en su vida diaria?
Hemos visto que, incluso si la función de onda cuántica es objetivamente real, es una onda de probabilidad, no una onda física. Por otra parte, la complementariedad y la incertidumbre implican que el electrón (o cualquier otra "partícula") no existe ni como una partícula física, ni como una onda física. Pero, en caso afirmativo, ¿en qué forma existe? Hasta ahora, hemos descuidado el papel del observador en todas las mediciones. Cuando tenemos en cuenta al observador (ver Capítulo 6), veremos que la teoría cuántica no necesita partículas ni ondas físicas (ver también la Sección 1.1), ¡pero necesita observaciones! Exploraremos esta asombrosa conclusión más adelante en capítulos posteriores.